Pendulum, << PEHN juh luhm or PEHN dyuh luhm. >> If a hanging object that pivots around a fixed point is pulled aside and let go, gravity makes it swing back and forth at a regular rate. Such a body is called a pendulum. The simple pendulum consists of a weight hanging at the end of a string or wire. The path traveled by the weight is called the arc of the pendulum. The period of oscillation is the time it takes the weight to pass back and forth once over this arc.
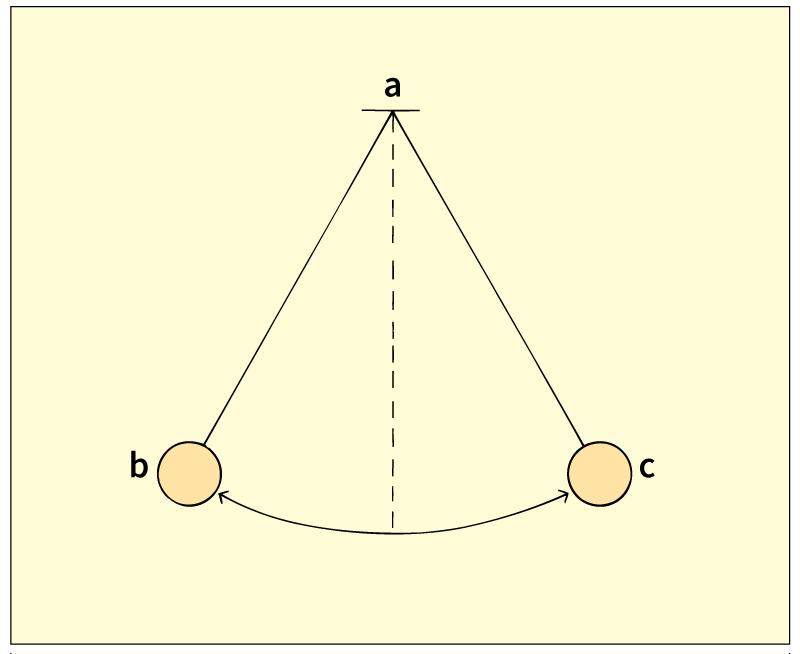
The period depends upon the pendulum’s length and location. If a pendulum were taken from one place to another on Earth, the period would change slightly due to a change in the pull of gravity. For example, the period would increase if the pendulum were taken from sea level to the top of a mountain. It increases because the force of gravity becomes weaker at greater heights. A simple pendulum 9.79 inches (24.87 centimeters) long has a period of 1 second at sea level.
If the swing is small, the period varies with the square root of the length of the pendulum. For example, the period of a 9-inch pendulum is 11/2 times as long as the period of a 4-inch pendulum. (The square root of 9 is 3, the square root of 4 is 2, and 3 is 11/2 times as large as 2.) The equation that expresses this relationship is:
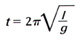
In this equation, t is time, the period of the pendulum, in seconds; l is the length of the pendulum in feet (meters); and g is the acceleration due to gravity, a factor that depends on the gravity where the pendulum is. At sea level,g = 32.16 feet (9,802 meters) per second per second.
The Italian physicist Galileo discovered the laws of the pendulum. He noticed that a hanging lamp would swing with an almost constant period, whether the arc was large or small. He believed that a pendulum could regulate the movements of clocks. The Dutch scientist Christiaan Huygens patented the first pendulum clock in 1657. Galileo’s observations are correct as long as the pendulum’s swing is small. However, the period of a pendulum increases when it has a large swing.
Clock pendulums
usually consist of a rod with a heavy weight at one end and a hard bearing at the other. A screw at the end of the rod permits the weight, or bob, to be raised or lowered. When the bob is lowered, the pendulum swings more slowly, and the clock runs more slowly. When the bob is raised, the pendulum swings faster, and the clock runs faster.
The bearing on which the pendulum swings must be as nearly frictionless as possible. It is often made of a knife edge of agate set in a grooved agate plate.
A device called an escapement is fastened to the mechanism of the clock. It gives small but regular pushes to the pendulum and keeps it swinging. The escapement lets one tooth of a toothed-wheel turn past it each time the pendulum swings aside. This action gives the clock its “ticktock” sound.
The rod in a clock pendulum tends to expand when it is warmed and to shorten when it is cooled. If no correction is made, pendulum clocks will run slower in hot weather and faster in cold weather. Several means have been developed to make up for this effect. For example, clocks known as regulators usually come with so-called gridiron pendulums. These pendulums consist of several brass and steel rods. The rods are arranged so that the brass rods raise the bob and the steel rods lower it as the temperature increases.

Other pendulums.
In torsion pendulums, a wheel or a balanced set of weights is suspended on a wire. The wire becomes twisted like a spring as the weight rotates around it. Torsion pendulums are used in the so-called 400-day clock and in other measuring instruments.
In bifilar << by FY luhr >> pendulums, two parallel wires hold the bob. They are pulled tight to provide a more controlled motion. A bifilar pendulum is sensitive to variations of the plumb line (line toward Earth’s center of gravity). Bifilar pendulums have been used to show that Earth does not rotate on its axis at a constant speed. Such changes in Earth’s rotation result from the pull of gravity exerted on the spinning Earth by the sun and moon.
In 1851, the French scientist Jean Foucault hung a large iron ball on a wire about 200 feet (60 meters) long. With this pendulum, he showed that Earth rotates on its axis. A Foucault pendulum is similar to a simple pendulum, but its motion is not limited to a plane. The plane of its swing appears to change as Earth goes through its daily rotation. However, the pendulum actually continues to move in the plane in which it was set in motion, while Earth turns under it. At the equator, a Foucault pendulum does not change its apparent plane of swing. The change would be fastest at the North and South poles (see Coriolis effect ).

