Percentage refers to computing by hundredths. You often see numbers such as 2%, 30%, and 75%. The % symbol means percent. You read the numbers “2 percent” “30 percent,” and “75 percent.” Percent means hundredths: 2% means 2 hundredths, 30% means 30 hundredths, and 75% means 75 hundredths. Percentages are really common fractions: 2% is 2/100, 30% is 30/100, and 75% is 75/100. Percentages are also decimal fractions: 2% is .02, 30% is .30, and, 75% is .75. Suppose you want to find 25% of 60. You must find 25/100, or .25, of 60. The term percent is from two Latin words meaning by the hundreds.
We use percentage frequently in everyday life. Bankers use percentage to compute interest on savings and loans. Our taxes are percentages of income, prices, and other amounts. Scientists often show the results of their observations and experiments with percentages. In baseball, team standings and batting averages are based on percentages. On clothing labels, percentages often represent the amounts of different fibers that are in the garment.
For hundreds of years, the business world has used the term percent, and this custom has persisted to the present time. The custom may come from Roman taxes, which were often stated as 1/20, 1/25, 1/100, and so on. In the Middle Ages, merchants commonly used hundredths and percentages even before the appearance of the decimal number system (see Decimal system ).
After the introduction of the decimal system, people no longer needed to use the term percent. It is just as easy to work with .25 as it is to work with 25%. However, percentage had become so deeply woven into business, professional, and everyday life that use of the term continued.
How to change percentages to fractions
Percent, in English, means hundredths. To change a percentage to a common or decimal fraction, you need only write the percentage as hundredths.
Changing percentages to common fractions.
To change a percentage to a common fraction, drop the % symbol and write in a denominator of 100. Here are four examples: 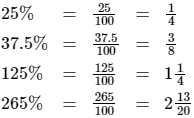
Changing percentages to decimal fractions.
To change a percentage to a decimal fraction, drop the % symbol and write in a decimal point two places to the left. Here are four examples: 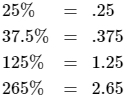
How to change fractions to percentages
Changing common fractions to percentages.
To change a common fraction to a percentage, divide the numerator by the denominator to get a decimal fraction. Then move the decimal point two places to the right and attach the % symbol. Here are four examples: 
Changing decimal fractions to percentages.
To change a decimal fraction to a percentage, move the decimal point two places to the right and attach the % symbol. Here are four examples: 
Solving percentage problems
Because percent means hundredths, you should restate any percentage problem in terms of decimal or common fractions. Then you can solve it fairly easily as a fraction problem.
How to find a percentage of a number.
Suppose you want to find 4% of 50. This means you want to find 4 hundredths of 50. First, change 4% to a common or decimal fraction. 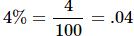
In order to find 4% of 50, you must multiply 50 by the fraction that 4% represents: 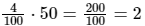
So 4% of 50 is 2.
Here are some more examples: 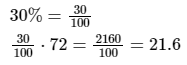
Find 30% of 72. 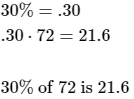
Find 662/3% of 915. 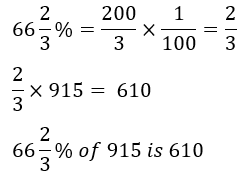
Find 250% of 32. 
What percentage is one number of another?
Look at the statement 20 = 4 X 5. The numbers 4 and 5 are factors of 20. When you multiply these factors, you get the product 20. Suppose the factor 5 is missing: 20 = 4 X ? . You can find the missing factor by dividing 20 by 4: 20 ÷ 4 = 5. Suppose the factor 4 is missing from the statement: 20 = ? X 5. You can find it the same way: 20 ÷ 5 = 4.
Now suppose one of the factors is a fraction. Look carefully at the problem 30 = ? X 1/4. You can find the missing factor by dividing 30 by 1/4: 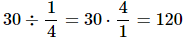
So 30 = 120 X 1/4. Percentages are hundredths, so you can use this process to find what percentage one number is of another.
Suppose you want to find what percentage of 30 the number 15 is. First, write the problem in the form 15 = ? X 30. You can find the missing factor by dividing 15 by 30: 
So 15 is 50% of 30.
Here are two more examples:
17 is what percentage of 340? 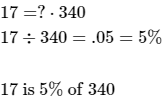
420 is what percentage of 70? 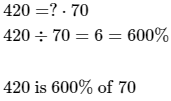
These problems can also be solved by comparing ratios. For example, in determining what percentage of 30 the number 15 is, you are attempting to find a number that compares to 100 in the same way that 15 compares to 30. That is, you are looking for the number that, with 100, expresses the same ratio as the ratio of 15 to 30: 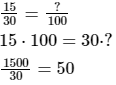
So 15 is 50% of 30.
Finding a number when a percentage is known.
Suppose you know that 6 is 25% of some number. What is the number? You can use the process of finding a missing factor to solve this problem. First, write the problem in the form 6 = 25% X ? . Now 25% is .25, so the problem becomes 6 = .25 X ? . You can find the missing factor by dividing 6 by .25: 6 ÷ .25 = 24
So 6 is 25% of 24.
Here are some more examples:
17 is 40% of what number?
17 = .40 X ?
17 ÷ .40 = 42.5
17 is 40% of 42.5
46 is 115% of what number?
46 = 1.15 X ?
46 ÷ 1.15 = 40
46 is 115% of 40
Applications of percentage
Commissions.
Many companies pay their salespeople by giving them a commission (a certain amount of money for each article they sell). The commission is usually a certain percentage of the price of the article that is sold.
Suppose a salesman receives a 15 percent commission on everything he sells. How much money does the salesman earn if he sells a refrigerator for $749? That is, what is 15 percent of $749? First, remember that 15 percent means 15 hundredths. You must find .15, or 15/100, of 749. 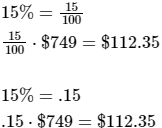
So the salesman earns $112.35 on the sale.
Comparisons.
Percentage gives us a method of comparing quantities. It helps to make a comparison where the relationship is not easy to see at once. For example, percentage helps people to compare volumes of sales on the stock market. Companies often use percentage to compare their business gains and losses. Engineers use percentage to compare production rates with their goals. Here is a more familiar example taken from the records of three baseball teams:
Boston Red Sox won 12 games and lost 8 games. Toronto Blue Jays won 13 games and lost 9 games. New York Yankees won 11 games and lost 6 games.
What is the correct standing of the teams?
To determine standing, you can compare the number of games won by each team to the number of games that team has played. First, you can see that the Boston Red Sox played 20 games and won 12 of them. What percentage of 20 is 12? Remember the process of finding a missing factor.
12 = ? X 20
12 ÷ 20 = .60
.60 = 60%
So the Boston team won 60 percent of its games.
The Toronto Blue Jays played 22 games and won 13 of them. What percentage of 22 is 13?
13 = ? X 22
13 ÷ 22 = .591
.591 = 59.1%
The Toronto team won 59.1 percent of its games.
The New York Yankees played 17 games and won 11 of them. What percentage of 17 is 11?
11 = ? X 17
11 ÷ 17 = .647
.647 = 64.7%
The New York team won 64.7% of its games.
Now you can arrange the teams on the basis of the percentage of games won:
New York Yankees, 64.7 Boston Red Sox, 60 Toronto Blue Jays, 59.1
You can use percentage to compare other quantities.
Interest.
When people borrow money from a bank, the bank charges them interest on the loan. Paying interest is like paying rent for the use of the money. Bankers usually compute interest by percentage.
Suppose a businesswoman borrows $6,000 from the bank. The bank charges her 9 percent interest a year. How much interest does she have to pay every month? First, what is 9 percent of $6,000?
9% = .09
.09 X $6000 = $540
9% of $6000 = $540
So the businesswoman must pay the bank $540 on her loan for one year. To find how much she must pay for one month, divide $540 by 12: $540 ÷ 12 = $45
So the businesswoman must pay the bank $45 every month as interest on her loan. See Interest .
Profits.
Businesses usually charge a price for an article that includes the article’s cost and the company’s own profit. This price is the selling price. Businesses usually compute their profits as percentages.
Suppose a dealer bought a bicycle from a manufacturer for $360. The dealer wants to make a profit of 25 percent of the price for which the bicycle is sold. How much must the dealer charge for the bicycle and what will the profit be? To make a profit of 25 percent, the cost of the bicycle from the manufacturer must be 75 percent of the price the dealer charges. So the problem is to find the number of which $360 is 75 percent. Remember the process of finding a missing factor.
75% = .75
$360 = ? X .75
$360 ÷ .75 = $480
$480 – $360 = $120
So the dealer must charge $480 for the bicycle. The profit will be $120. As a check, you can see that the profit, $120, is 25 percent (or one-fourth) of the selling price of $480.
Taxes.
Many prices include taxes. For example, the price of a bracelet could include both federal and state tax charges. These taxes are usually computed as percentages of an article’s price before the tax was added.
Suppose a college sells tickets for a football game. Each ticket costs $30. The $30 price includes a 10 percent federal tax on the college’s income from the ticket. What is the income from each ticket? If the $30 price includes both income and the 10 percent tax, then the $30 must represent 110 percent of the income. So the problem is to find the number of which $30 is 110 percent.
110% = 1.10
$30 = ? X 1.10
$30 ÷ 1.10 = $27.27 (to the nearest cent)
So the income that the college earns from each ticket sold is $27.27.
