Permutations and combinations are names that mathematicians use for certain groups of objects or symbols. Permutations are ordered arrangements of a set of objects. For example, ABC, ACB, and BAC are three permutations of the set of symbols A, B, and C. Combinations are those groups that include the same objects regardless of the order in which they are arranged. The sets ABC, ACB, and BAC are all examples of the same combination. Sets such as ABC, ABD, and ACD are examples of different combinations.
The branch of mathematics that includes permutations and combinations is called combinatorics. Combinatorics has many uses, including the routing of telephone calls through cables and the scheduling of production in factories. It has become an area of active research as computers have grown in importance.
Counting permutations
The question, “How many sets of letters can be formed from the three letters A, B, and C?” is the same as the question, “How many permutations are there of 3 objects taken 3 at a time?” You can find the answer (1) by making a list of all the possibilities, (2) by reasoning, and (3) by using mathematical formulas.
By listing.
To find the answer by listing, you merely write down all the possibilities and count them. The list below shows there are 6 possibilities. Therefore there are 6 permutations of 3 objects taken 3 at a time.
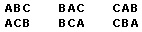
You could also list the possibilities in the form of a tree diagram that shows the choices for each position:
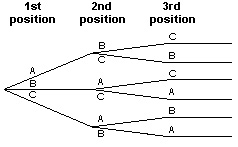
The diagram again shows that you can form 6 sets.
By reasoning.
You could also find the number of permutations by reasoning. For the first position, you have 3 possible choices, A or B or C. With each of these choices, you have only 2 possible choices left for the second position, and 3 X 2 = 6. With each of these 6, you have 1 possible choice for the third position, and 6 X 1 = 6. Therefore, the number of possible sets of letters is 3 X 2 X 1 = 6.
Using reason is better than just listing the permutations because reasoning accounts for every possibility. In listing, you might forget to include some possibilities, especially if you had a large number of objects.
Suppose, for example, that you had 26 letters instead of only the letters A, B, and C, and that you were asked to find the total number of sets of 3 letters that could be formed. Listing all the possibilities would be difficult and tedious. But finding the answer by reasoning would be easy. With every one of the 26 possible choices for the first position, there would be 25 choices for the second position. This makes a total of 650 possibilities (26 X 25 = 650). With each of these 650 choices, there would be 24 letters remaining as possible choices for the third position, making a total of 15,600 possible combinations (650 X 24 = 15,600). The total number of permutations is therefore 26 X 25 X 24 = 15,600.
The above example illustrates the multiplication principle for permutations: If the first position can be filled in n ways, and the second can be filled in n-1 ways, and the third in n-2 ways, then the total number of permutations in the three positions is n X (n-1) X (n-2).
Suppose you had only A’s, B’s, and C’s, but at least 3 of each. How many sets of 3 initials could you form? (The sets would include AAA, AAB, ABB, and so on.) In this example, each position could be filled in 3 different ways, and so you could calculate the answer: 3 X 3 X 3 = 27 sets. With 26 letters and at least 3 of each, you could form 26 X 26 X 26 = 17,576 sets.
By using symbols and formulas.
In mathematical terms, the number of permutations of n things taken r at a time is represented by the symbol nPr). Using this symbol, you can express the answers to permutation problems as follows:
3 things (such as A, B, and C) taken 3 at a time 3P3 = 3 X 2 X 1 = 6
26 things taken 3 at a time 26P3 = 26 X 25 X 24 = 15,600
n things taken r at a time nPr = n(n – 1)(n -2) … [n – (r – 1)]
The last expression is the general formula. The bracketed quantity, [n – (r – 1)], means n minus the quantity (r – 1). Algebraically, this quantity is the same as (n – r + 1). This quantity tells you at what point to stop writing successive multipliers in the formula. For example, if n is 26 and r is 3, then (n – r + 1) = 26 – 3 + 1 = 24 and so the multipliers for 26P3 are 26 X 25 X 24.
Solving combination problems
If you had 4 books, how many sets of 3 books could you form? This question is the same as the question, “How many combinations are there of 4 things taken 3 at a time?” Suppose, for example, that the 4 books were written respectively by Adams, Beery, Cole, and Doe. If you chose books by Adams, Beery, and Cole, your reading material would be the same regardless of the order in which you read the books. Thus, there is only 1 combination of these 3 books taken 3 at a time. How many other 3-book combinations could you make from the 4 books? As in the permutation problem above, you can find the answer (1) by listing the possibilities, (2) by reasoning, and (3) by using mathematical formulas.
By listing.
For simplicity, represent the 4 books by the letters A, B, C, and D. Write down several groups of these 4 letters, and then cross out one letter at a time, always leaving a group of 3. You would cross out a different letter each time so that the remaining group would always be a different combination.
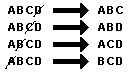
The list shows that there are 4 possible combinations.
By reasoning.
A knowledge of permutations enables you to arrive at the answer in the following way. You can select any 3 of the books in 6 different orders, for example, ABC, ACB, BAC, BCA, CAB, CBA. But these 6 permutations represent only a single combination. You can conclude that there are 6 permutations for each different combination of 3 books. Therefore, the total number of permutations must be equal to 6 times the number of possible combinations. Likewise, the number of possible combinations must be equal to the total number of permutations divided by 6. The total number of permutations of 4 books taken 3 at a time is 4P3 = 4 X 3 X 2 = 24
The number of permutations for each combination of 3 books is 3P3 = 3 X 2 X 1 = 6
Therefore, the number of possible combinations is 24 ÷ 6 = 4.
Suppose you want to count how many combinations of 3 different letters could be in a spoonful of alphabet soup. In the section of this article on counting permutations, we calculated that the total number of permutations of 26 letters taken 3 at a time is 26 X 25 X 24 = 15,600. We also calculated that the number of permutations for each combination of 3 letters is 3 X 2 X 1 = 6. Therefore, the number of possible combinations in our spoonful of soup is 15,600 ÷ 6 = 2,600.
By using symbols and formulas.
The number of combinations of n objects taken r at a time is represented by the symbol nCr. In the book example, the number of possible combinations can be expressed and calculated as follows:
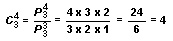
The general formual for combinations is
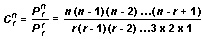
For example, if n = 6 and r = 4,
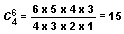
Mathematicians simplify the formula for nCr by using factorial notation to represent the product of a positive whole number with all the positive whole numbers less than itself. Factorial 3 means 3 X 2 X 1, and it is written 3!. Likewise, 4! means 4 X 3 X 2 X 1. Permutation formulas can therefore be simplified as follows:
3P3 = 3!
4P4 = 4!
rPr = r!
The simplified combination formula is
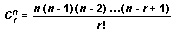
Mathematicians simplify the above formula even more and write it as follows:
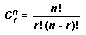
The last two formulas are the same because
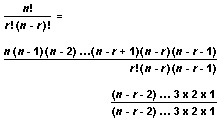
All factors in this expression can be divided out except for n(n – 1)(n – 2) … (n – r + 1) in the numerator and r! in the denominator. These are the same factors that appear in the original combination formula.
With the two forms of the combination formula, you can calculate the number of possible combinations in two ways. For example, if you had 5 books from which to choose a set of 3, you could find the number of combinations as follows:
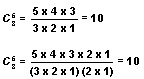
If you divide out factors in the numerator and denominator of the above expressions, you will see that they are identical. See also Factor .
History
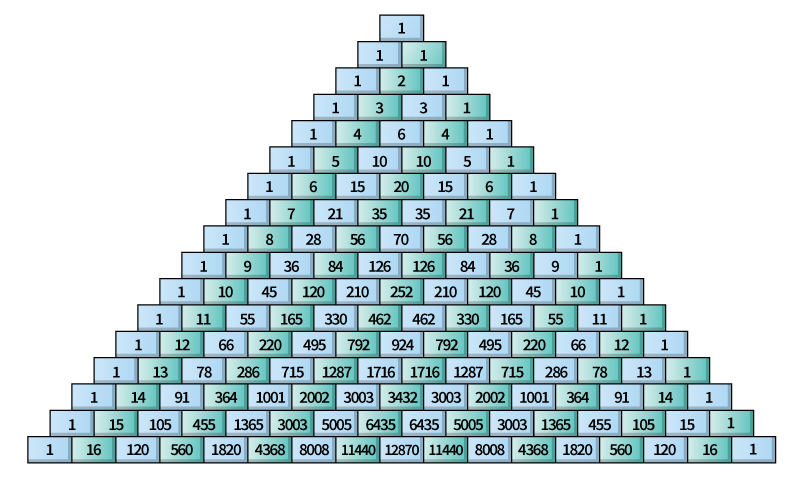
The real development of mathematical thought about permutations began in the 1600’s with the development of the theory of probability. About this time, the French mathematician Blaise Pascal discovered an interesting device for computing combinations. The device, called the Pascal triangle, is shown in the illustration. Pascal constructed the triangle so that each number was the sum of the two numbers above it. The numbers, called elements, are arranged in rows. Each element has a place in a row determined by counting from left to right. Thus, 20 appears in the 4th place of the 7th row of the triangle.
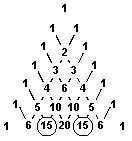
Pascal found that the element in the (r + 1)th place of the (n + 1)th row is the same as the number of combinations of n things taken r at a time (nCr). If n is 6 and r is 2, the number of combinations is given in the 7th row, the 3rd place (15, as circled). But 15 also appears in the 5th place of the 7th row (dashed circle). Because the triangle is symmetrical, the element that is in the (r + 1)th place of the (n + 1)th row is always the same as the element in the (n – r) + 1)th place of that row. Therefore, nCr = nCn – r For example, if n is 6 and r is 2, the same number of combinations is possible if the objects are taken 2 or 4 at a time.
