Addition is a way of putting together two or more things to find out how many there are all together. Only like things can be added. This is, you cannot add apples and pencils together.
Suppose you have a set of 5 apples and a set of 3 apples on a table:

Now put the sets together in a new set of 8 apples.

You add when you put together two or more sets to find out how many there are all together.
Learning to add
To find out how many things you have added to make a new set, you can count them or think them together.
Addition by counting.
Ralph has 3 red marbles and 4 blue marbles. He puts them together in one set.

How many marbles are there in the first set? Count them. There are 3 marbles. How many marbles are there in the second set? Count them. There are 4 marbles. Now, put the marbles together and count them in the third set. There are 7 marbles. We call this counting together. You counted to find how many 3 marbles and 4 marbles are together. You discovered that 3 and 4 are 7.
Suppose you have drawn 3 circles. Now draw 4 more circles next to the first 3.

You know that there were already 3 circles. So you can think “3” and point to each of the 4 new circles, and count “4, 5, 6, 7.” This is called counting on. You can find out how many 3 and 4 are together by thinking “3” for the first set, and counting on until you have counted the 4 circles in the second set. Counting on serves as a quicker way of adding things than counting them together.
Addition by thinking.
Suppose there are 4 girls at the blackboard and 5 girls at the reading table. You find how many girls there are all together by thinking. For example, you could think: “I already know that 4 and 4 are 8, so 4 and 5 will be 1 more. That means that 4 and 5 are 9.” Or, you could think: “4 girls and 5 girls are 9 girls.” We call this thinking together. Thinking together is a quicker way of adding than counting together or counting on.
Regrouping.
Suppose you want to put together two sets in a new set and the new set will be more than 10. For example, Nancy wanted to know how many 9 and 6 are. To find out, she drew a number line:

Then, she drew lines to show 9 and 6 as shown below:

Nancy found out that 9 and 6 are 15. But she saw something interesting and drew two more lines:

Nancy found that 9 and 6 are the same as 10 and 5. It is easier for beginners to add 10 and 5 than it is to add 9 and 6. We call changing the sets 9 and 6 to the sets 5 and 10 regrouping. Here are some examples:
8 and 4 are 12 (10 and 2)
7 and 8 are 15 (10 and 5)
9 and 4 are 13 (10 and 3)
Writing addition.
You should write down your addition problems, so you have a record of your counting or thinking.
You can make a record with pictures:

Or you can make a record with numbers and words: 2 and 4 are 6
But it is easiest and best to make a record with numbers and signs:
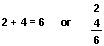
In the first example, the plus sign (+) tells you to add. You can read 2 + 4 as “two and four.” The equals sign (=) means that the sets on one side of the sign are equal to the set on the other side of the sign. You can read 2 + 4 = 6 as “two and four are six.” The second example shows how you write an addition problem when you want to work out the answer on paper. The two or more groups you want to put together, or add, are called addends. The new group is called the sum.
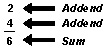
Addition facts.
By putting together sets, you have discovered that 5 + 3 = 8, 3 + 4 = 7, and 9 + 6 = 15. We call these addition facts. Each addition fact is made up of two addends and a sum. You can discover all the addition facts by putting together sets of things. Some beginners practice with sets of pennies or bottle caps.
It is best to learn the addition facts so you can use them quickly and easily. You will be able to use them in your daily life. You will also need them to add larger numbers and solve problems.
Learning these addition facts looks like work at first. But there are several ways to make learning the facts easier. For instance, if you look at all the facts in which a number and 1 are added, you will see that learning them is something like ordinary counting. Also, many of the pairs of addends are just the reverse of each other. For example, 4 + 5 adds up to the same thing as 5 + 4. We call a fact like 3 + 3 = 6 a double. Knowing doubles is useful. If you know that 4 + 4 = 8, then 4 + 3 is 1 less than 8, and 4 + 5 is 1 more than 8. You should be able to think of other ways to help you learn the addition facts.
Adding larger numbers
You use the addition facts and the idea of place value to add larger numbers.
Adding 10’s.
Last week, Tom earned 2 dimes, or 20¢. This week, Tom earned 3 dimes, or 30¢. How much has Tom earned all together? You can find the answer by counting:

You find that Tom earned 5 dimes, or 50¢. You can find the answer by adding.

If you know that 2 + 3 = 5, you know that 2 dimes and 3 dimes are 5 dimes. A dime is 10¢, so you can see that 20¢ + 30¢ = 50¢.
Here is another example:
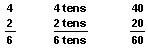
You can see that 4 + 2 = 6, 4 tens + 2 tens = 6 tens, and 40 + 20 = 60. The 6 in the 60 shows six 10’s because it is in the 10’s place. You add 10’s the same way you add 1’s. But you must write the sum in the 10’s place. And you must remember to write a zero in the 1’s place to show that the sum is 10’s, not 1’s.
Here is a third example:
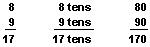
Here the sum of the 10’s is seventeen 10’s. Seventeen 10’s is the same as ten 10’s and seven 10’s. But ten 10’s is 100. So you must write the sum in the 10’s and 100’s places, and write in a zero to show that the answer is one 100, seven 10’s, and no 1’s.
Adding 10’s and 1’s.
Suppose there are 23 boys and 24 girls in a school play. To find out how many children there are all together, you must add 23 and 24.
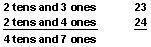
We call the numbers 23 and 24 two-place numbers. When you add two-place numbers, you add the 1’s first. In this example, three 1’s and four 1’s are 3 + 4 = 7. You write the sum of the 1’s in the 1’s place of the answer:
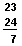
Next, you add the 10’s. Two 10’s and two 10’s are added as 2 + 2 = 4. The 4 stands for four 10’s. You write the sum of the 10’s in the 10’s place of the answer:

So there are 47 children in the school play.
Here is another example:

First, you add the 1’s: 2 + 3 = 5. Next, you find that seven 10’s and four 10’s are eleven 10’s. Eleven 10’s are the same as ten 10’s and one 10, or one 100 and one 10. So you must write the sum of the 10’s in the 10’s and 100’s places in the answer.
When there are several addends, we often speak of the 1’s, 10’s, and 100’s as columns. When you add columns, you must learn to think the additions. At first it may help to keep some kind of record.

With practice, adding two-place numbers and long columns will be easy.
How to carry.
When you add two-place numbers, the sum of the 1’s column is often 10 or more. To add such numbers, you must learn to carry.
Here is an example of carrying:

You add longer columns the same way.
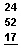
First, add the 1’s column: 4 + 2 = 6, and 6 + 7 = 13. Thirteen is one 10 and three 1’s. Write the 3 in the 1’s place of the answer. Carry the one 10 to the 10’s column by writing a 1 at the top of the 10’s column.
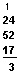
Now add the 10’s column: 1 + 2 = 3, 3 + 5 = 8, and 8 + 1 = 9. This 9 means nine 10’s. Write the 9 in the 10’s place.
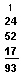
Adding three-place and four-place numbers is no more difficult than the examples you have just done. You must always remember to keep the columns straight, and to add 1’s, 10’s, 100’s, and so on, in order. Here is an example:

First, add the 1’s column: 1 + 3 + 9 = 13. Write 3 for three 1’s in the 1’s place of the answer. Carry the 10 by writing 1 for one 10 at the top of the 10’s column.
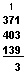
Next, add the 10’s column: 1 + 7 + 0 + 3 = 11. This is not eleven 1’s. It is eleven 10’s. Eleven 10’s is one 100 and one 10. So write 1 for the one 10 in the 10’s place of the answer. Carry the 100 by writing 1 for one 100 at the top of the 100’s column.

Now add the 100’s column: 1 + 3 + 4 + 1 = 9. This 9 is nine 100’s. Write 9 in the 100’s place of the answer.

The sum is 913. You use the same method of carrying for 1,000’s and larger numbers.
Here is an example in which the number you carry is more than one 10:

First, add the 1’s column: 7 + 9 + 8 = 24. Twenty-four is two 10’s and four 1’s. Write the 4 in the 1’s place in the answer. Carry the two 10’s to the 10’s column by writing a 2 at the top of the 10’s column.

Now add the 10’s column: 2 + 3 + 2 + 1 = 8. This 8 means eight 10’s. Write the 8 in the 10’s place of the answer.

The sum is 84. The numbers you carry may often be 20’s or 30’s or 40’s, and so on.
Checking addition
Good workers always check their addition to see if they have made any mistakes. There are several ways to check addition.
Adding up.
You have learned to add a column of figures by starting at the top and adding down. After you have written the sum, you can check your answer by adding up. That is, starting at the bottom of the column and adding up to the top. Here is an example:

If you get the same answer adding up as you did adding down, your answer is probably right.
Subtraction
can be used to check problems with only two addends (see Subtraction). Here is an example:
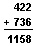
To check the addition, subtract one of the addends from the sum. For example, subtract 736 from 1,158. The subtraction should leave 422 if the addition is correct.
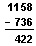
Estimating
is a good way of checking addition, but it will not catch small mistakes. If you estimate before you work a problem, you will have an idea of your answer in advance. You should get into the habit of always estimating your answer first. Here is an example:

There are other methods of checking used in arithmetic. Some of them can be used for addition.
Addition rules to remember
- Remember what addition means. You can find the answers to addition problems by counting. But it is quicker and easier to think the answers.
- Learning the 81 addition facts will help you think the answers to addition problems.
- You can put the addends in any order without changing the sum of the equation. For example, 3 + 2 + 7 = 12, 2 + 7 + 3 = 12, and 7 + 3 + 2 = 12.
- You can add only quantities of the same kind. That is, you must add 1’s to 1’s and 10’s to 10’s, and be careful not to mix them up.
Fun with addition
Two winks.
Make a pack of 20 cards on which the numbers from 1 to 10 have been written. Make two cards for each number. Divide the pack of cards into two piles, and put one pile face down in front of each player. The first player turns a card and holds it up for both players to see. The second player does the same thing from the other pile of cards. The player who first sees that the sum of the numbers on the two cards is 10 or more calls out “Two winks!” Then, that player takes the two cards. If the two cards do not equal 10 or more, the players put them back in the piles. The game continues, with two new players turning the cards. When all of the cards have been turned, the player with the most cards wins.

Tick-tack-toe puzzle.
Each player draws a tick-tack-toe figure on a piece of paper.
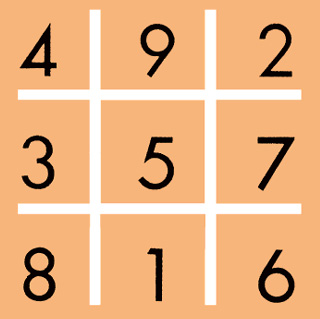
Then, each tries to fill in the spaces with the numbers from 1 to 9, so that if three numbers are added across, up and down, or diagonally the sums will be 15. The player must use each number from 1 to 9. The first player with the correct answer wins.
