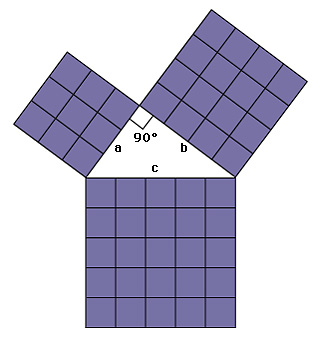
Pythagorean theorem, << pih `thag` uh REE uhn THEE uhr uhm, >> in geometry, states that in a right triangle the square of the length of the hypotenuse equals the sum of the squares of the lengths of the other two sides. The square of a number is the number multiplied by itself. A right triangle is one in which one angle measures 90°. The hypotenuse is the side opposite the right angle. The Pythagorean theorem written as a formula is: c2 = a2 + b2
In this formula, c is the length of the hypotenuse, and a and b are the lengths of the other two sides. If you know the lengths of any two sides of a right triangle, you can find the length of the third side.
Origins.
The ancient Egyptians wanted fields with square (90°) corners. They had few of the tools we have today. How could they make a 90° angle? About 2000 B.C., they discovered a “magic 3–4–5” triangle. Workmen knotted a loop of rope into 12 equal spaces. They stretched the rope around three stakes to form a triangle. They placed the stakes so the triangle had sides of 3, 4, and 5 units. The angle opposite the side of 5 units (the hypotenuse) measured 90°.
The ancient Babylonians noticed a special characteristic of the numbers of the 3–4–5 triangle. They saw that 32 + 42 = 52 (9 + 16 = 25). The Babylonians found other groups of three numbers that had this characteristic.
Between 500 and 350 B.C., a group of Greek philosophers called the Pythagoreans came to regard the sides of the 3–4–5 triangle as the sides of three squares. They knew that the area of any square is the length of a side multiplied by itself. Thus, they saw that the area of the square on the hypotenuse equals the sum of the areas of the squares on the other two sides. They also discovered that this relationship among squares is true for all right triangles. They stated this in the rule that became known as the Pythagorean theorem.
A proof.
The Pythagorean theorem has had many geometric proofs, but no one knows which proof the Pythagoreans developed. Some mathematicians believe it was a dissection proof, like the one decribed below.
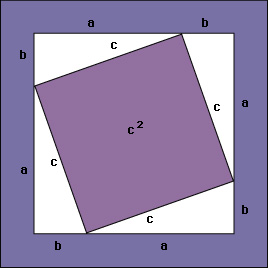
In the drawing shown below, the two smaller sides (a and b) of a right triangle together equal the side of a large square. This square is divided into four right triangles, in which c is the hypotenuse, and two smaller, colored squares are a2 and b2.
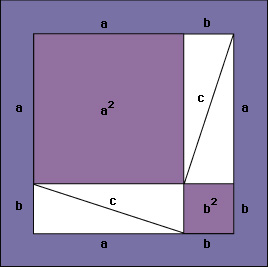
In the next drawing, the triangles have been rearranged so that their hypotenuses form the sides of a colored square. The area of the newly formed square is c2. The area of both large squares is the same because each has a side equal to a + b. In the two large squares, the triangles occupy equal areas. Therefore, the colored portions of the two large squares occupy equal areas, and so a2 + b2 = c2.