Set theory is a way of solving problems in mathematics and logic (reasoning). By studying set theory, you can get a better understanding of arithmetic and of mathematics as a whole.
A set is a collection of objects or ideas. For example, a family, a box of crayons, a flock of sheep, the rules of a game, and the even numbers from 10 to 20 are all sets. The items that make up a set are the members or elements of the set. A red crayon is a member of a set of crayons. The number 16 is a member of the set of even numbers from 10 to 20.
Mathematicians use letters to name sets and the members of sets. Capital letters commonly represent sets, and lower-case letters refer to the members of sets. For example, the letter C might stand for the set of fifth-grade girls with curly hair. The letters m, s, and r might represent the members of this set—Martha, Sara, and Ruth.
A common way to define a set is to enclose the symbols that represent its members in braces {}. Thus, you would write: C = {Martha, Sara, Ruth} or simply C = {m,s,r}.
The symbol ∊ indicates that a member belongs to a certain set. For example, s ∊ C is read: “s is a member of C.” To show that j does not belong to C, write j ∉ C, which is read: “j is not a member of C.”
In addition to defining a set by its members, mathematicians may also define it in terms of its properties. A property is a characteristic that relates the members of a set to one another. In the example above, C has three properties: (1) its members are girls, (2) its members are in the fifth grade, and (3) its members have curly hair. To define the set by these properties, you would write: C = {x x is a fifth-grade girl with curly hair}. This statement is read: “C is the set of all members, x, such that x is a fifth-grade girl with curly hair.” The line between the two x’s means “such that.”
Mathematicians also use various combinations of circles and rectangles to define sets, show relationships, and solve problems. Such drawings are called Venn diagrams or Euler’s circles.
Kinds of sets
In working with set theory, mathematicians compare one set with another. Mathematicians have given names to various kinds of sets to aid in the comparisons. Ten major kinds of sets are (1) universal, (2) finite, (3) infinite, (4) empty, (5) single element, (6) equivalent, (7) equal, (8) overlapping, (9) disjoint, and (10) subsets. Every set can be called by more than one of these names.
Universal sets
consist of all members being considered at any one time. Mathematicians call such a set a universe and usually represent it by the letter U. For example, if a certain problem deals with only the whole numbers from 1 to 10, then U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. In another problem, the universe might be all girls in the fifth grade or all even numbers. The Venn diagram of the universal set is shown below.

Finite sets and infinite sets.
A finite set has a definite number of members. “Three cats” and “three thousand head of cattle” are finite sets. An infinite set has an endless number of members. For example, the numerals you use in counting form an infinite set. They include 1, 2, 3, 4, 5, and so on without end. It is impossible to list all the members of an infinite set. One way to represent such a set is to list the first few members and then write three dots: {1, 2, 3, … }.
Empty sets,
also called null sets, have no members. The following sets show which students were absent from school on three days. Monday: Paul, Frances. Tuesday: Joe. Wednesday: No one absent. The Monday set of absentees has two members and the Tuesday set has one member. The Wednesday set has no members; it is an empty set. To show an empty set, leave a blank space between a pair of braces, or write the symbol ∅. Thus, students absent on Wednesday = { } = ∅.
Single element sets
contain only one member. In the example above, the set of students absent on Tuesday, {Joe}, is a single element set.
Equivalent sets
have the same number of members. For example, if there are four desks and four students in a classroom, the set of desks is equivalent to the set of students. To show that A and B are equivalent, write: A ↔ B. The symbol ↔ is read: “is equivalent to.”
Equal sets
have the same members. Suppose that the set of students who received 100 per cent on a spelling test is S = {Pete, Mark, Joan, Tom}. Suppose further that the set of students who received 100 per cent on an arithmetic test is A = {Tom, Joan, Pete, Mark}. S is equal to A because the sets have the same members. To indicate that the sets are equal, you would write: S = A.
Overlapping sets and disjoint sets.
Overlapping sets have some members in common. If the set of last year’s class officers is L = {Dick, Susan, Betty} and the set of this year’s officers is T = {Mark, Susan, Tom}, sets L and T overlap because Susan belongs to both sets.
Disjoint sets have no members in common. Suppose the set of students running for office next year is N = {Patty, Carmen, Jim}. Set N is disjoint from L and T because it does not have any elements in common.
The Venn diagram below shows the relationships between sets L, T, and N.
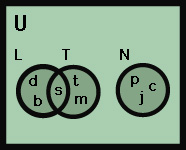
Subsets
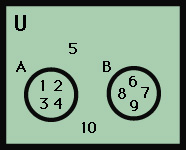
are contained within other sets. For example, the set of fifth-grade girls with curly hair is a subset of the set of all fifth-graders. In another example, consider the universe of {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. If set A = {1, 2, 3, 4} and set B = {6, 7, 8, 9}, then A and B are subsets of the set U. To show this, you write A ⊂ U and B ⊂ U. The symbol ⊂ is read: “is included in.” Subsets A and B are finite sets because they have a definite number of members. Subsets A and B are also equivalent sets because they have the same number of members, and they are disjoint sets because no members belong to both A and B.
Using set theory
In algebra,
sets are helpful in understanding and solving problems. Suppose that in a certain problem the letter x stands for any number from 1 to 10 and you are to find what the value or values of x are under certain conditions. In this problem, x is a variable and the set of numbers from 1 to 10 is the domain of the variable. The solution is the set of all numbers in the domain that make a true statement when substituted for x under the conditions given. Such a set is called a solution set.
Suppose, for example, that the domain of x is U = {4, 5, 6, 7, 8, 9} and you are to find the values of x, such that (1) x can be divided evenly by 2, or (2) x can be divided evenly by 3. The word or connecting the two conditions means you need the union (combination) of the solutions for the two conditions. This combination is written A ∪ B, which is read: “A union B.”
To solve this problem, divide each member of the domain by 2. Then use your results to define the solution set for the first condition thus: A = {4, 6, 8}. Next, divide each member of the domain by 3 and define the solution set for the second condition as B = {6, 9}. The solution set for the whole problem is A ∪ B, which equals {4, 6, 8, 9}, as shown by the shaded area in the Venn diagram below.
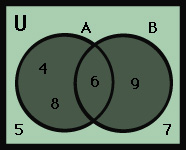
Depending on the problem, a solution set may be an empty set, or it may have any number of members. See Algebra (Learning algebra) .
When the conditions of a problem are connected by the word and, the solution set is the intersection (overlap) of the solutions for the conditions. This set is written A ∩ B, which is read “A intersect B.” Suppose, as in the previous problem, the domain of x is U = {4, 5, 6, 7, 8, 9}, but this time you are to find the values of x, such that (1) x can be divided evenly by two, and (2) x can be divided evenly by three. In solving the solution sets for the conditions, you again find A = {4, 6, 8} and B = {6, 9}. However, this time the solution set for the whole problem is A ∩ B, which equals {6}, as shown by the shaded area in the diagram below.
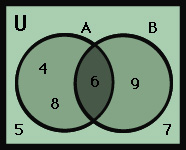
In logic,
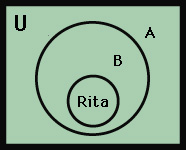
set theory can help you form conclusions based on statements called premises. Suppose, for example, a logic problem has two premises: (1) All sixth-grade girls are members of the school glee club, and (2) Rita is a sixth-grade girl. Suppose you are to determine whether Rita is a member of the club.
To solve this problem using set theory, let A be the set of members of the school glee club, and let B be the set of girls in the sixth grade. According to the first premise, B is a subset of A. That is, every member of B is a member of A. According to the second premise, Rita belongs to set B. Therefore, Rita must also belong to set A. Thus, you conclude that she is a member of the school glee club. The Venn diagram for this problem is shown below.
History
The set theory studied in elementary and high schools developed from two mathematical discoveries of the 1800’s—symbolic logic and the theory of sets.
Symbolic logic is a way of using mathematical symbols and operations to solve problems in logic. George Boole (1815-1864), an English mathematician, established the basis of this technique in the 1840’s.
In the 1870’s, the German mathematician Georg Cantor (1845-1918) applied some of the ideas of symbolic logic to sets of numbers. He formed a theory that he called “the theory of sets.” Cantor developed this theory because of his interest in infinite quantities.
Cantor explored the idea that two sets can have a one-to-one (1:1) correspondence with each other. For example, the set {1, 2, 3} and the set {a, b, c} have a 1:1 correspondence, because each element in one set can be paired with exactly one element from the other. Infinite sets can also have 1:1 correspondences. For example, the set of counting numbers and the set of even numbers can be matched one-to-one as follows:
1, 2, 3, 4, 5, and so on; 2, 4, 6, 8, 10, and so on.
The two sets appear to be equally numerous—even though the counting numbers contain many numbers that are not even. Cantor embraced this seeming paradox (contradiction). He defined an infinite set as a set that can be matched one-to-one with a part of itself. This idea revolutionized the study of infinity.
Cantor also showed that not all infinite sets have the same “size,” or cardinality. For example, the set of real numbers—that is, all the points that form the number line—cannot be matched one-to-one with the counting numbers. The real numbers are said to be “uncountably infinite.” The set of real numbers thus has a greater cardinality than “countably infinite” sets that can be matched one-to-one with the counting numbers.
