Topology, a branch of mathematics, deals with certain properties of geometric figures that cannot be changed by stretching, squeezing, or twisting the figures. Rather than studying an object’s exact shape, as in traditional geometry, topologists examine fundamental characteristics shared by abstract “families” of shapes.
Invariance and equivalence
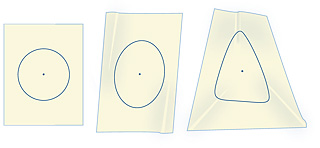
are two key concepts in topology. Certain properties of geometric figures remain the same after stretching, squeezing, or shrinking the figures, without tearing or joining. For example, imagine you have drawn a circle with a dot inside it on a thin sheet of rubber. By stretching the rubber, you can easily change the circle into an oval, square, or triangle. However, no amount of stretching will put the dot outside the circle. The dot’s location in the interior of the figure is topologically invariant (unchanging). Furthermore, the circle, oval, square, and triangle have the same invariant properties. They are therefore topologically equivalent.
Equivalence and invariance also apply to three-dimensional figures. Imagine, for example, playing with a doughnut made of soft clay. By stretching and pinching—but not tearing or joining—you could mold the doughnut into a coffee mug or vice versa. Notice that the hole in the doughnut remains as the hole in the handle of the coffee mug. The hole is thus invariant. Further, because they share the invariant properties, the doughnut and coffee mug are topologically equivalent. Topologists routinely apply equivalence and invariance to abstract objects of even more dimensions.

Algebraic topology
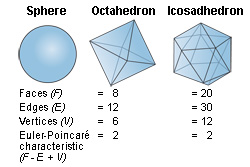
uses the techniques of algebra to investigate topological invariance and equivalence. One example of an invariant from algebraic topology is called the Euler characteristic. This characteristic is a number that can be assigned to a geometric figure whose surface has been triangulated (broken up into triangular faces). Topologists count the number of faces (F), the number of edges (E), and the number of vertices or corners (V). The Euler characteristic equals F — E + V.
Consider, for example, two triangulations of a sphere: the octahedron and the icosahedron. Both figures have an Euler characteristic of 2. In fact, no matter how a surface is triangulated, the characteristic remains invariant. More importantly, two shapes with the same Euler characteristic are always topologically equivalent. The characteristic takes its name from the Swiss mathematician Leonhard Euler, who proved that the characteristic remains invariant.
Geometric puzzles
have contributed to the development and popularization of topology. One famous such puzzle is sometimes called the three-cottage problem. Imagine three cottages and three utility buildings that provide gas, water, and electric power. Each cottage must be connected to all three of the utilities, but the connecting lines may not cross one another or pass through any building. Is it possible for all three cottages to receive all three services? Using topology, mathematicians can show that it is not possible on a plane or the surface of a sphere but that it is possible on a doughnut- shaped surface.
Applications.
Though abstract, topology has many applications. When designing electronic circuit boards, electrical engineers solve more complicated versions of the three-cottage problem. Other applications of topology can be found in chemistry, economics, computer science, physics, and other branches of mathematics.
History.
Topology began in earnest in the 1800’s with the work of the German mathematicians Carl Friedrich Gauss and Georg Friedrich Bernhard Riemann. The French mathematician Henri Poincaré gave the first systematic treatment of topology in his paper “Analysis Situs” (1895). He also introduced algebraic topology. Important developments in topology continued through the 1900’s all the way to the present. In 1976, for example, mathematicians proved the four-color theorem with the help of computers. The theorem states that four colors are sufficient to color any map so that no two adjacent countries are the same color. In the early 2000’s, the Russian mathematician Grigori Perelman completed a proof of the Poincaré conjecture, one of the most famous and difficult problems in topology and in all of mathematics. The conjecture, proposed by Poincaré in 1904, deals with topological equivalence in abstract, three-dimensional figures.
