Trigonometry, << `trihg` uh NOM uh tree, >> is a branch of mathematics that deals with the relationships between the sides and angles of triangles. It also provides methods of measuring these sides and angles. Trigonometry has applications in such theoretical sciences as physics and astronomy, and in such practical fields as surveying and navigation. The word trigonometry comes from two Greek words meaning triangle and measure.
There are two kinds of trigonometry—plane trigonometry and spherical trigonometry. Plane trigonometry is used to determine the unknown sides and angles of triangles that lie in a plane. Spherical trigonometry can be used to find the unknown sides and angles of triangles that lie on a spherical surface.
Both types of trigonometry are based on relationships that exist between the six parts—three sides and three angles—of any triangle. Because of these relationships, in almost all cases any three parts whose measures are known can be used to find the measures of the other three parts, if at least one of the known parts is a side. It is necessary to know the length of at least one side because the corresponding sides of two triangles may be unequal even though all their corresponding angles are equal.
Trigonometry is based on a type of geometry called Euclidean geometry. Euclidean geometry was developed from a set of assumptions spelled out about 300 B.C. by the Greek mathematician Euclid (see Geometry (Types of geometry) ). The Greek astronomer Hipparchus, who lived during the 100’s B.C., made important contributions to trigonometry.
Plane trigonometry
To understand trigonometry, it is necessary first to study the properties of similar triangles. Two triangles are said to be similar when all the corresponding angles of the triangles are equal. For example, the triangles GHI and JKL shown here are similar if angle G = angle J, angle H = angle K, and angle I = angle L. The corresponding sides of similar triangles need not be equal. However, they are in proportion. Therefore, if triangles GHI and JKL are similar, the ratio GH:GI will equal the ratio JK:JL. Suppose that GH = 3 units, GI = 5 units, and JK = 9 units. Then JL = 15 units, because 3/5 = 9/15.
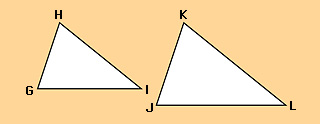
Right triangles.
Trigonometry is largely derived from the study of similar right triangles. A right triangle is any triangle in which one of the angles equals 90°. The three angles in any triangle total 180°. Therefore, every right triangle has two acute angles that total 90°. If we know one of the acute angles, we can find the other one by subtracting the known angle from 90°. In addition, if an acute angle of one right triangle equals an acute angle of a second right triangle, then the two triangles are similar. In the right triangles ABC and DEF shown here, for example, angle C and angle F are right angles and angle A equals angle D. Therefore, the two triangles are similar. And because they are similar, their sides must be in proportion, so that
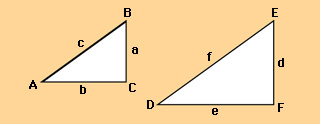
The ratios that make up these proportions will equal the ratios for the corresponding sides of any right triangle that has an acute angle equal to angle A. Each of the possible ratios between the sides of a right triangle has been given a special name. In the illustration above, for example, the ratio
Trigonometric tables also include three rarely used ratios called the secant, cosecant, and cotangent. The secant of angle A, written sec A, is
Following are formal definitions of the six trigonometric ratios:

The trigonometric ratios make it possible to find all three sides of the right triangle ABC if we know the measure of one of the acute angles and the length of any side. For instance, if angle A is 30°, then we can use a table or calculator to determine that sin A =
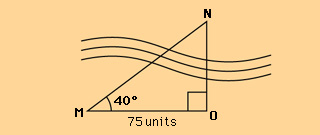
This method has many applications. For example, suppose you are standing at point O on the bank of a river and looking at a tree at point N on the opposite shore (see the figure accompanying this paragraph). You can use this method to find the distance from O to N without crossing the river. First, place a marker at point O. Then, walk along a line at right angles to the line NO until you come to a convenient point M, thus forming the right triangle MNO. Next, measure the length of the line MO. If MO is, say, 75 units long, and angle M measures 40°, you can use a calculator or table to determine that tan 40° = 0.8391. Because tan M =
The law of sines.
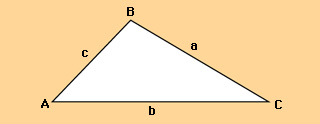
For some applications, you must determine the unknown parts of a triangle that is not a right triangle. If you know two angles and one side of such a triangle, you can find the other two sides and the other angle by using the law of sines. This law says:
For a triangle ABC with sides a, b, and c,

If we know angle A and angle B, we can determine angle C, because angle C = 180° – (angle A + angle B).
If we know side c, we can then find sides a and b, because from the law of sines we know that
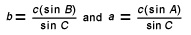
The law of cosines.
If we know two sides of a triangle that is not a right triangle, and the angle between them, the remaining parts of the triangle can be found by using the law of cosines. The law of cosines states:
For a triangle ABC with sides a, b, and c,
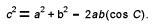
For example, if we know sides a and b and angle C, we can find side c by the law of cosines. We can then use the law of sines to find the other two angles. Thus, if side a = 5 units, side b = 7 units, and angle C = 52°, we can solve for the unknown side and angles of the triangle. Using a table or a calculator, we can determine that cos 52° = 0.6157. We can then use the law of cosines to solve for c 2:

Then, we calculate that c = the square root of 30.901 = 5.56 units. Next, because we know from the law of sines that
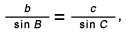
we find that (sin B) c = b (sin C).
Therefore,
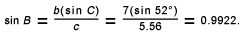
Using a table or a calculator, we can then determine that angle B = 82.8°. Finally, angle A = 180° – (82.8° + 52°) = 45.2°.
A special case.
There is only one case in which we must know more than the measures of three parts of a triangle to solve for the triangle’s unknown sides and angles. This case occurs when we know two sides and one angle, but the known angle is not between the two known sides. In such a case, the triangle could take two possible forms. In the figure below, for example, if we know only angle G and sides g and i, then the triangle may be either triangle GHI or triangle GHI’.
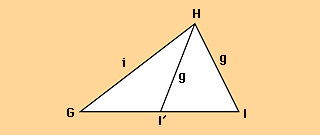
The two possibilities for the angle opposite side i are GIH and GI’H. These two angles are supplementary—that is, they total 180°. Sines of supplementary angles are equal, so sin angle GIH = sin angle GI’H. Thus, we cannot use the law of sines to determine which angle is part of the unknown triangle. To solve the triangle, we must know whether the triangle has an obtuse angle or whether all its angles are acute. If it has an obtuse angle, the triangle is GHI’. If all its angles are acute, the triangle is GHI. Once this extra information is provided, we can use the law of sines to determine the remaining parts of the triangle.
Spherical trigonometry
On the surface of a sphere, the shortest path between two points is an arc of the circle that contains those two points and whose center is the center of the sphere. Such a circle is called a great circle. On a globe, the circles of longitude, which pass through the North Pole and the South Pole, are great circles. The circles of latitude, except for the equator, are not great circles because their centers lie above or below the center of the sphere. Arcs of circles are measured in degrees. A complete circle measures 360 degrees. The circumference of a great circle on the earth is about 24,860 miles (40,008 kilometers). Thus, each degree of arc of a great circle on the earth extends about 69.06 miles (111.13 kilometers). The angle between two great circles is the angle between their tangents at the point of intersection. A tangent is a line that touches an arc at one point only, without intersecting it. A spherical triangle is formed by the intersections of three great circles.
Because both the angles and the sides of a spherical triangle are measured in degrees, the formulas of spherical trigonometry differ somewhat from the formulas of plane trigonometry. Also, spherical triangles differ from plane triangles in that the angles of a spherical triangle always total more than 180°. However, spherical trigonometry uses the same tables that plane trigonometry uses.
The basic formulas in spherical trigonometry are the law of sines for spherical triangles, which reads:

and the law of cosines for spherical triangles, which reads:

The figure below shows how these laws are applied. The distance from New York City to Paris is calculated by drawing a spherical triangle whose vertices are New York City, Paris, and the North Pole.
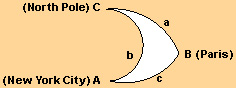
Because the longitude of Paris is 2.20° east and the longitude of New York City is 73.58° west, angle C is 2.20° + 73.58°, or 75.78°. Because the latitude of Paris is 48.51° north, arc a is 90° – 48.51°, or 41.49°. Because the latitude of New York City is 40.40° north, arc b is 90° – 40.40°, or 49.60°. By the law of cosines for spherical triangles, the measure of arc c can be found by using the equation:

We can use a table or calculator to determine that .60942 is the cosine of a 52.45° arc. Therefore, arc c is 52.45°, and the distance from New York City to Paris is 69.06 miles (111.13 kilometers) x 52.45, or 3,622 miles (5,829 kilometers).
To find the direction in which Paris lies in relation to New York City, we find the measure of angle A by using the law of sines for spherical triangles:
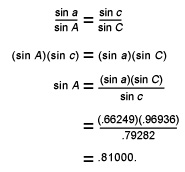
We can use a table or calculator to determine that angle A is 54.1°. From New York City, therefore, the compass direction to Paris is 54.1° east of north. But the angle between the direction to Paris and the north changes as a person travels along the great circle from New York City to Paris. Therefore, a person cannot reach Paris by simply traveling in this compass direction.
