Fibonacci sequence, << fee buh NAH chee, >> is an interesting series of numbers named for the Italian mathematician who introduced it. The Fibonacci sequence begins as follows:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
Two 1’s start the sequence. Each number after that is the sum of the two numbers before it. For example, the 8 in the sequence comes from adding the two numbers before it, 5 and 3. The 89 is the result of adding 55 and 34. The sequence goes on forever. Numbers in the sequence are called Fibonacci numbers. Leonardo Fibonacci introduced the sequence in a math problem in his book Liber Abbaci (1202). The Fibonacci sequence seems relatively simple. But mathematicians have uncovered surprising patterns in the sequence.
Sums in the sequence
reveal one interesting pattern. If you add up the first n Fibonacci numbers, the sum is equal to the second number after n in the sequence, minus one.
For example, consider a case in which n = 6. The first six Fibonacci numbers add up to 20:
1 + 1 + 2 + 3 + 5 + 8 = 20.
Now look two numbers ahead of n, at the eighth number in the Fibonacci sequence: 21. The sum of the first six numbers does in fact equal one less than the eighth number. Similarly, the sum of the first seven numbers, 33, is one less than the ninth number in the sequence, 34—and so on.
The golden ratio,
also called the divine proportion, figures into another amazing property of the Fibonacci sequence. The golden ratio is a number that appears in many areas of math, nature, and art. The golden ratio is:
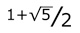
which is equal to about 1.61803.
If any Fibonacci number is divided by the number immediately before it, the result gets progressively closer to the golden ratio. For example, divide the seventh number by the sixth number:
Now divide the eighth number by the seventh number:
21 ÷ 13 = 1.61538…
And so on. The further along the sequence you go, the closer the result gets to the golden ratio. But because the sequence goes on forever, it only approaches the golden ratio, never actually equaling it. The German astronomer and mathematician Johannes Kepler discovered this pattern in the Fibonacci sequence.
Appearance in nature.
Just as the golden ratio appears in nature, so do Fibonacci numbers. For example, the kernels of a pine cone form two sets of spirals. One set runs clockwise, and the other set runs counterclockwise. The number of spirals in each set is always a Fibonacci number, usually 8, 13, or 21. This pattern is a natural consequence of mathematical principles that underlie the plant’s growth.
See also Fibonacci, Leonardo .
