Complex number is a number with two components: a real part and an imaginary part. Complex numbers are usually written in the form a + bi or a + ib. In this expression, a and b represent real numbers. Real numbers include positive and negative counting numbers and fractions. They also include irrational numbers (numbers that cannot be written as a fraction), such as pi (π) and the square root of 2. The imaginary unit, i, is not a real number. It equals the square root of –1 [see Square root (Square roots of negative numbers) ]. Imaginary numbers are not imaginary in the sense of being “made-up.” Mathematicians in the 1500’s came up with the name “imaginary,” and it is still used today.
We call the number a the real part of the complex number. The number b—or sometimes the quantity bi—is called the imaginary part. Examples of complex numbers are 2 + 3i and 1/2 – 2/5 i. The imaginary number 7i is also a complex number, because we can write it as 0 + 7i. Similarly, the real number 3 is also the complex number 3 + 0i. Thus, the set of complex numbers includes all real and all purely imaginary numbers.
In arithmetic.
We can add, subtract, multiply, and divide complex numbers, just like real numbers. However, two additional rules apply to complex numbers. First, i 2 should always be replaced by –1. Second, the final result should always be written as a + bi.
Here is one example of complex arithmetic:
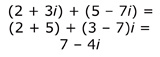
In the example, we find the sum of 2 + 3i and 5 – 7i by adding the real parts of each number (2 + 5) and the real numbers in the imaginary parts (3 – 7). The result is 7 – 4i.
Representing complex numbers.
Real numbers can be represented visually as points on a number line. Complex numbers, on the other hand, can be represented using a system of coordinates on a graph. Such coordinates are often written in the form (x, y)—with x marking a point’s horizontal position and y marking its vertical position. A point with coordinates (a, b) would correspond to the complex number a + bi.
Alternatively, mathematicians may represent complex numbers as vectors. A vector is a line segment that extends in a particular direction. The vector for a particular complex number starts at the origin of the graph—coordinates (0, 0)—and extends in the direction of the point (a, b).
History.
Early mathematicians gave imaginary numbers their name because they were confused as to whether or not such numbers really existed. In the late 1700’s, scholars gradually began to accept imaginary and complex numbers into mathematics. Such numbers have numerous practical applications in physics and engineering. For example, engineers use complex numbers in calculations dealing with mechanical vibrations and electric circuits.
