Number, in mathematics, represents a quantity or an amount. A number can tell how many objects there are in a certain set, as in one apple or five letters. Numbers can also describe the order of objects—for example, the third planet from the sun. In addition, numbers can measure properties (characteristics) of objects, such as an object’s length, weight, or temperature.
By themselves, numbers are just ideas. But we can write or discuss numbers using symbols called numerals. For example, several different numerals can represent the number we think of as twelve. They include the decimal numeral 12, the Roman numeral XII, and the binary numeral 1100. These three numerals all represent the same idea—the number twelve. Decimal, Roman, and binary are three kinds of numeral systems. Numeral systems, also called systems of numeration, are ways of counting and naming numbers.
Numeral systems
Numeral systems differ in the symbols they use. They also differ in the way they group symbols to represent larger numbers.
The decimal system
is the most commonly used numeral system. It uses 10 numerals, called digits. They are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The decimal system is also called the base ten system. The word decimal comes from the Latin word deca, meaning ten.
The decimal system represents larger numbers using groups of 10. Suppose you want to count how many pennies you have saved. You could stack them in groups of 10 pennies each. If there are 10 or more such stacks, you can bunch the piles together to form an even larger group of 10 tens—or 100—pennies.

In this picture, there are eight (8) single pennies, four (4) stacks of 10 pennies, and two (2) groups of 100 pennies. Thus, we say there are 248 pennies. The decimal number 248 is organized the same way as the pennies. It is short for saying that there are 2 hundreds, 4 tens, and 8 single pennies.
The decimal system is an example of a place-value system, also called a positional system. That is, the value of each digit in a decimal number depends on its place. In the number 248, the 2 is in the hundreds place. It actually means 200. The 4 is in the tens place. It means 40. The 8 is in the ones place. It simply means 8.
The digit 0 has special importance in the decimal system. It lets us show that a certain place is empty. For example, the decimal number 205 means 2 hundreds, no tens, and 5 ones. Ancient numeral systems lacked a symbol for zero. They thus found it difficult to represent numbers using place values.
In the decimal system, each place represents a power of 10. In mathematics, the word power means the result of multiplying a number by itself a certain number of times. For example, 10 to the third power—written 103 —means 10 × 10 × 10. The following table shows several place values and their corresponding powers of 10:

The 2 in 102, the 3 in 103, and so on are called exponents. The number 10 is called the base. This is why the decimal system is also called the base 10 system.
There is no particular mathematical reason to base a numeral system on the number 10. Rather, the decimal system likely began simply because humans have 10 fingers for counting. In fact, the word digit means finger.
The binary system
only uses two digits—generally 1 and 0. It is also called the base two system. The word binary comes from a Latin word meaning two at a time. Computers use binary numbers for processing information and performing other basic functions.
The binary system, like the decimal system, uses places. But in the binary system, the places are powers of 2, not 10. For example, the binary number 10 means 1 two, not 1 ten. The binary number 11 means 1 two and 1 one. This adds up to the decimal number 3. The following table shows several place values in the binary system and the corresponding powers of two:

In the decimal system, the number 1101 means 1 thousand, 1 hundred, 0 tens, and 1 one. But in binary, the places are powers of 2, not of 10. So the binary number 1101 means 1 eight, 1 four, no twos, and 1 one. The binary number 1101 is thus equal to the decimal number 13.
Roman numerals
express numbers using letters, such as M (1,000), C (100), X (10), V (5), and I (1). This system does not make use of place value. Instead, the individual values are often added together. For example, the Roman numeral VII is equal to the decimal number 7 (5 + 1 + 1). See Roman numerals .
Kinds of numbers
The numbers discussed so far are all members of the set of natural numbers. There are infinitely many natural numbers. Even so, math uses many more numbers.
Natural and whole numbers.
Natural numbers are also called counting numbers or positive integers. They are the numbers 1, 2, 3, and so on. The set of whole numbers is often said to include the natural numbers, plus zero. Some mathematicians include zero with the natural numbers.
Integers.
The set of integers includes zero and all the natural numbers along with their negatives. It can be written: {… –3, –2, –1, 0, 1, 2, 3, …}. The integers go on forever in both directions. Negative integers are not part of the set of natural numbers.
Rational numbers.
Integers, along with natural and whole numbers, have one feature in common: their members are separated by “gaps” of one whole unit, with nothing in between. But in daily life, we must often represent quantities between two integers—for example, half a loaf of bread or a distance of two and a quarter miles.
We can represent such quantities using the set of rational numbers. This set includes all the ratios of integers. Half a loaf of bread can be expressed using the rational number 1/2. Ratios written in this way are also called fractions. Two and a quarter miles can be expressed using the number 2 1/4, or 9/4.
The integer –7 is also a rational number, because it can be written as –7/1. Thus, the set of rational numbers includes every integer. Any two integers, when divided, produce a rational number—with one exception. Division by zero is impossible.
Every rational number can be written as either a terminating decimal—one that ends—or a repeating decimal. For example, 3/4 is equal to a decimal, 0.75, which terminates (ends). The number 4/33 equals a repeating decimal, 0.121212…. The pattern of alternating 1’s and 2’s repeats forever.
Irrational numbers.
The set of rational numbers seems large. But even it has many “gaps” between its members. Many numbers, called irrational numbers, cannot be written as ratios of integers. The most famous irrational number is the number pi (π). Pi is the ratio of a circle’s circumference to its diameter. No fraction of integers describes this quantity.
Unlike a rational number, an irrational number can be represented by a nonterminating, nonrepeating decimal. No group of digits in such a number repeats itself in exactly the same order. For example, the first eight decimal digits of π are 3.1415927. But the digits go on forever after that, with no pattern.
Real numbers.
If we combine all rational and irrational numbers, we get the larger set of the real numbers. This set is “complete“ in the sense that there are no more gaps between its members.
Complex numbers.
In advanced mathematics, there is a still larger set of numbers, the complex numbers. Complex numbers take the form a + bi. In this formula, a and b are real numbers. The quantity i equals the square root of –1 . No real number, when multiplied by itself, results in a negative number. Thus, the quantity i is called the imaginary unit. The word “imaginary” does not mean the number is made-up or fictional. Nor does the word “real” mean that real numbers are more real than other numbers.
Examples of complex numbers include 3 + 2i and –5 + i. The real number 7 is also a complex number, because it can be written as 7 + 0i. Likewise, 4i is a complex number. It can be written 0 + 4i.
Thus, the real numbers are a subset of the complex numbers. Likewise, the rational numbers are a subset of the real numbers. The integers are a subset of the rational numbers. Each set is a subset of the next one.
History
Ancient people had several ways of recording the few numbers they needed. A shepherd, for example, could collect pebbles to represent the number of sheep in a flock. Each pebble meant one sheep. A bag of pebbles stood for the whole flock.
Later, people developed other ways to record the number of their possessions. They tied knots in a leather thong or scratched tally marks on the side of a rock. They then matched the knots or marks against each item. Later, people began to use words to represent numbers. These words described “how many” and helped people match items mentally. For example, people used the word for “wings” to mean two objects. For five items, they used the word that meant “hand.”
Finally, people began to count by arranging the names of numbers in a certain order. To count, they spoke or wrote the word that meant “one,” next the word for “two,” then the word for “three,” and so on. In time, people in many parts of the world developed various kinds of counting systems. Some were based on 5, others on 10, and still others on 12 or 60. People still use such measures as 12 inches in a foot and 60 minutes in an hour, descended from these ancient systems.
In most early numeral systems, people formed numerals simply by repeating basic symbols and adding the values to get the number they wanted. The Egyptians, Greeks, and Romans used systems of this kind. The Maya of Central America and the Hindus of India used systems that followed the principle of place value. These systems used a symbol that meant “not any,” a forerunner of our modern zero. The Hindu system ultimately developed into the decimal numeral system.
The Egyptians.
About 3000 B.C., the ancient Egyptians used hieroglyphics (picture writing) to write numerals, as shown below.
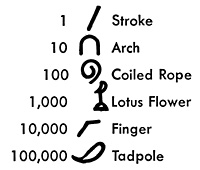
The Egyptian system was based on 10. But it did not include a zero symbol. Nor did it use the principle of place value. The Egyptians formed numerals by putting basic symbols together. For example, they wrote the numeral 1,326 like this:
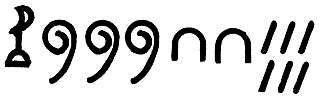
The Mesopotamians,
who lived in what is now Iraq, used cuneiform (wedge-shaped) symbols to write numbers. As early as 3000 B.C., they developed a system based on the number 60. A numeral contained groups of symbols. One group stood for the number of ones, the next group stood for 60’s, the next for 3600’s (60 × 60), and so on.
The Greeks.
About 500 B.C., the Greeks developed a system based on 10. This system used a 27-letter Greek alphabet—the present-day 24-letter alphabet plus 3 letters no longer used. The first 9 letters stood for numbers, from 1 through 9. The next 9 letters stood for tens, from 10 through 90. The last 9 letters were symbols for hundreds, from 100 through 900.
The Greek philosopher Pythagoras, who lived about 550 B.C., explored beyond the representation of numbers to their very nature. Pythagoras believed that everything could be understood in terms of whole numbers or their ratios. About 400 B.C., however, the Greeks discovered irrational numbers. They recognized that Pythagoras’s ideas were incomplete.
The Romans
used letters as symbols for numbers. But the early Roman system of about 500 B.C. differed from the system we use today. For example, the ancient Romans wrote 4 as IIII and 9 as VIIII. Today, we usually use IV for 4 and IX for 9. A table of Roman numerals appears in the World Book article Roman numerals . People throughout Europe widely used Roman numerals until the A.D. 1500’s. The numerals are still used on clock faces, in outlines, and for other purposes.
The Chinese,
by the 100’s B.C., had devised a decimal system of numbers. It included fractions, zero, and negative numbers.
The Maya
used a numeral system based on 20. A dot represented the number one, and a bar represented five. The Maya system was a place-value system, and the Maya used a zero before A.D. 600. Their system was as advanced as the systems that gave rise to the modern decimal system.
The Hindu-Arabic numeral system.
Hindu mathematicians of the 300’s and 200’s B.C. used a system based on 10. The Hindus had symbols for each number from one to nine. They had a name for each power of 10, and used these names when writing numerals. For example, Hindus wrote “1 sata, 3 dasan, 5” to represent the number we write as 135. They wrote “1 sata, 5” for the number we write as 105.
The Hindus gradually developed a way of eliminating place names. They invented the symbol sunya (meaning empty), which we call zero. With this symbol, they could write “105” instead of “1 sata, 5.”
During the 700’s, the Arabs learned Hindu arithmetic. In the 800’s, a Persian mathematician named al-Khwarizmi wrote a book that used the Hindu numeral system. His book was translated into Latin about 300 years later. This translation brought the Hindu-Arabic numerals into Europe. Modern decimal numerals are sometimes called Arabic numerals for this reason.
Several centuries passed before the Hindu-Arabic system became widely used. After Europeans learned to print from movable type in the 1400’s, they published many mathematics textbooks. Most of the books showed calculations using the Hindu-Arabic system. These books brought the system into widespread use.
Binary numbers.
During the late 1600’s, the German mathematician and philosopher Gottfried Wilhelm Leibniz developed the binary numeral system. However, mathematicians found no practical use for the system until the 1940’s, when computers were developed. Computers and other electronic devices used the binary system because they could represent any number with circuits that were in one of two states, on or off.
Beyond real numbers.
In the 1500’s, mathematicians first encountered imaginary numbers. They gave the numbers the name “imaginary” because they were confused about the nature of the numbers. In the late 1700’s, scholars gradually began to accept imaginary and complex numbers into mathematics. Such numbers have numerous practical applications in physics and engineering. For example, engineers use complex numbers in calculations dealing with mechanical vibrations and electric circuits.
