Fraction is a part of something. When objects are measured, often the measurements do not come out in whole units. A book may weigh between 2 and 3 pounds. The amount over 2 pounds is a fraction of a pound. A board may measure between 10 and 11 inches long. It is 10 inches plus a fraction of an inch long. The word fraction comes from a Latin word meaning to break. Fractions result from breaking a unit up into a number of equal parts. A unit can be broken into any number of parts. If you break a stick into two pieces, however, you do not necessarily have two halves of the stick. In order to have two halves of the stick, you must break it into two pieces of equal length.
Fractions are written in numerical form as two numerals separated by a line: 2/5.
In arithmetic, a fraction generally stands for the number of equal parts into which something has been divided and the number of those parts that are being considered. For example, the fraction 2/5 represents two parts of something that has been divided into five equal parts.
The fraction form is also used for (1) expressing division, (2) representing a ratio, and (3) stating a rate. In expressing division, the fraction 2/5 may indicate two divided by five—for example, dividing two candy bars equally among five people. A ratio is a comparison of two quantities that are both measured in the same units. A ratio may compare a part to a whole or a part to another part. For example, if there are two girls and three boys on a debating team, the ratio of girls (a part) to team members (the whole) is two to five (2/5). The ratio of girls (a part) to boys (another part) on the team is two to three (2/3). In mathematics, any number that can be written as the ratio of two whole numbers is called a rational number (see Ratio). Rate is the relation between two quantities that are measured in different units. For example, a basketball team may score at the rate of two goals per every five minutes of play.
The different uses and meanings of fractions are closely related. Often, understanding one of the meanings of fractions will help make understanding other uses easier. This article concentrates on the meaning of fractions as parts of a whole and examines the use of fractions in arithmetic.
Expressing fractions
In words.
The names for fractions come from the number of equal parts into which a whole unit has been divided. In English, there are special names for the fractional parts formed when a unit is divided into two, three, or four equal parts. When a unit is broken into two equal parts, each part is called a half. When it is broken into three equal parts, each part is called a third. And when it is broken into four equal parts, each part is called a quarter or a fourth. The names for other fractional parts are made by adding –th to the end of the word that tells the number of equal parts into which the unit has been broken. For example, the fractional parts made by breaking a mile into 10 equal parts are called tenths of a mile.
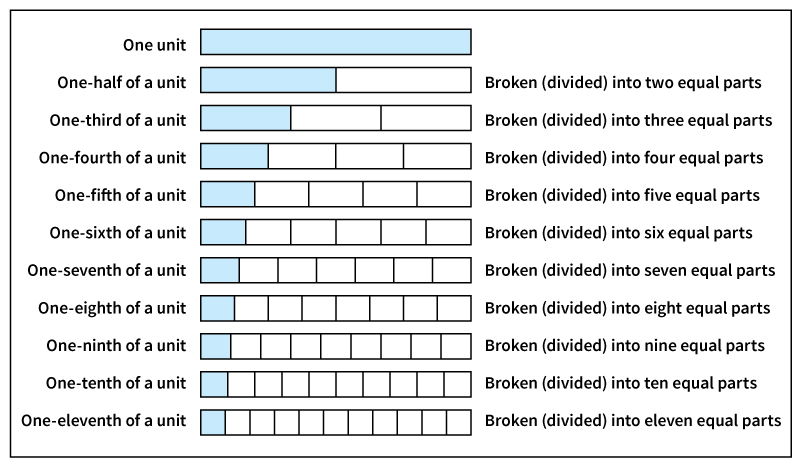
As a unit is broken into more and more equal parts, each part gets smaller and smaller. But the fraction names make it sound as though the parts were getting larger and larger. The –th in sixth, for instance, means that each part is one of six equal parts of a whole unit. If the same unit were broken into 12 equal parts, each part would be a twelfth. Although a twelfth may sound larger than a sixth, each twelfth actually is only half as big as each sixth. The larger-sounding fraction name means that the original unit has been broken into more—and thus smaller—parts.
The number word before the fraction name tells how many of the fractional parts are being considered. For example, five-sixths represents five of the sixths into which something has been broken. Six-sixths means that a unit has been divided into six equal parts, and all six parts are being considered. Therefore, six-sixths equals one whole unit. Similarly, seven-sevenths, eight-eighths, nine-ninths, and so on all equal one.
In symbols.
When fractions are written in numerical form, the bottom, or second, numeral is called the denominator (namer). It provides the name of the fraction, telling the number of equal parts into which the unit has been broken. The top, or first, numeral is called the numerator (numberer). It tells how many of the fractional parts are being considered. The numerator and the denominator are called the terms of a fraction.
Fractions such as 4/10, 7/100, and 5/1,000 are called decimal fractions. Decimal fractions have denominators of 10 or 10 multiplied by itself a number of times. Decimal fractions can be written without a denominator by using the decimal system. In this system, the value of each decimal place in a figure is 10 times smaller than that of the place to its left. For example, the first place to the right of the decimal point is the 1/10 ‘s (tenths) place. The second place to the right of the decimal point is the 1/100 ‘s (hundredths) place. When decimal fractions are written using the decimal system, the number of parts into which the unit has been divided is indicated by the number of decimal places used. The numerals that are in the decimal places used represent the number of parts that are being considered. For example, the fraction 7/10 may be written as 0.7 in the decimal system. Twenty-seven hundredths is written as 0.27. For information on changing fractions to decimals and changing decimals to fractions, see Decimal system (Decimals and fractions).
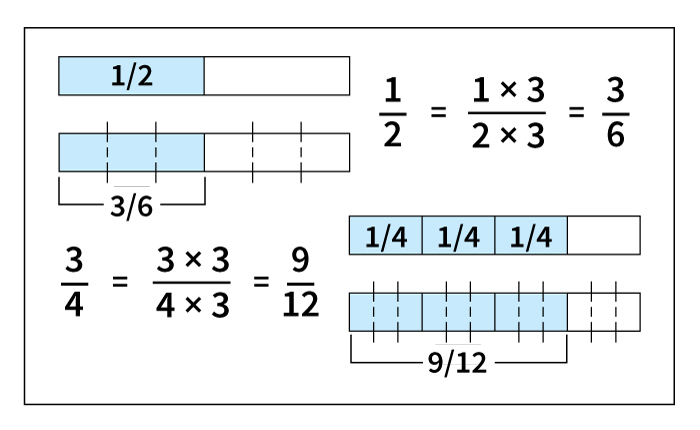
Equivalent fractions
When two fractions have different numerators and denominators but still express the same part of a whole, they are called equivalent fractions. The chart on the following page shows several equivalent fractions.
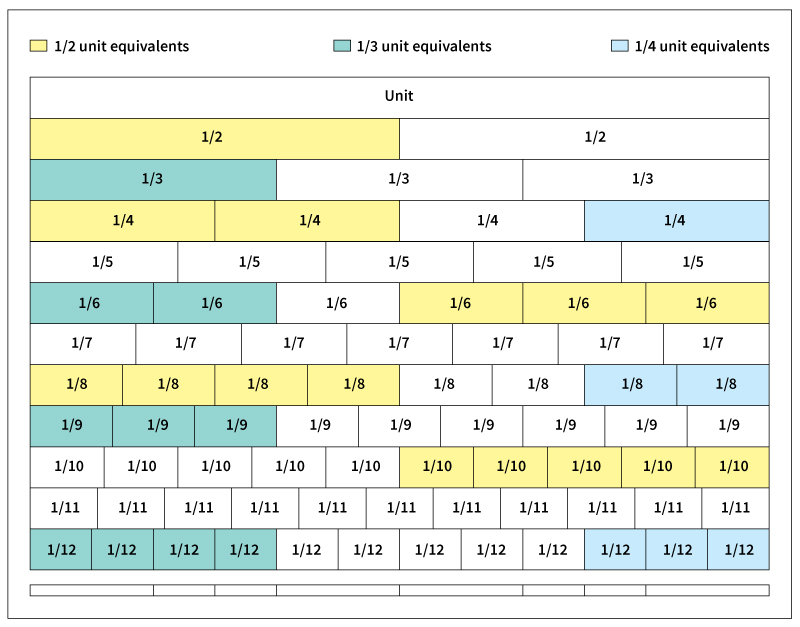
If you compare the part of the whole unit formed by 1/2 with the part formed by two 1/4 ‘s, you can see that they have the same length. When 1/2 of the original unit is broken into two equal parts, each of those new parts is 1/4 of the whole unit. Three 1/6 ‘s are the same as 1/2 broken into three equal parts, four 1/8 ‘s are 1/2 broken into four equal parts, and so on.
Breaking each part of a fraction into more equal parts is the same as multiplying the numerator and the denominator of that fraction by the same number. Multiplying the numerator and denominator of a fraction by the same number produces an equivalent fraction that has larger numbers in both the numerator and denominator.
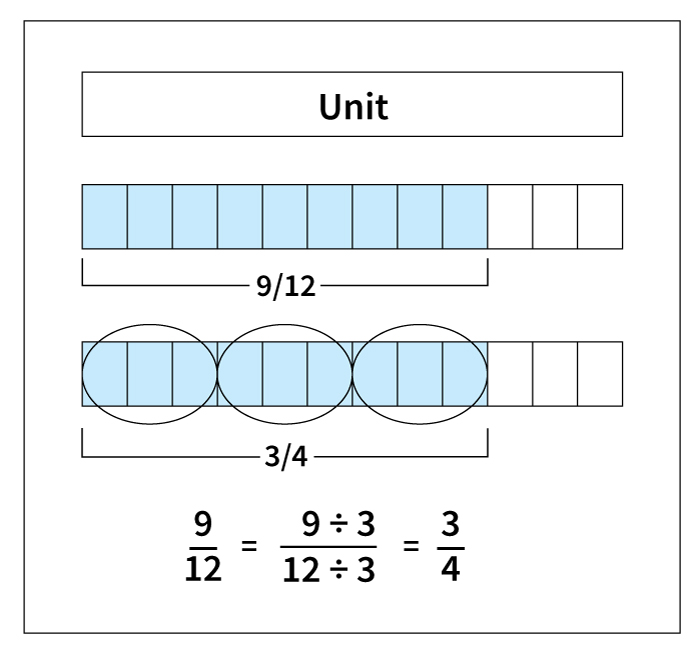
To make an equivalent fraction with smaller numbers in both numerator and denominator, divide the numerator and denominator by the same number. 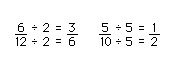
Finding an equivalent fraction with smaller numbers in the numerator and the denominator is called reducing the fraction. When no number except 1 can be used to divide both the numerator and denominator evenly, the fraction is said to be reduced to its lowest terms.
Comparing fractions
When two fractions have the same denominator, it is easy to tell which fraction is larger. The fraction with the larger number in the numerator is larger, because more parts of the unit are being considered. For instance, 5/7 of something is larger than 3/7 of that same thing.
When two fractions have different denominators, it is more difficult to find out which fraction is larger. To compare fractions with different denominators, change the fractions into equivalent fractions. This process is called finding a common denominator. An easy way of finding a common denominator is to multiply the two original denominators and use that product as the common denominator. Then, multiply the numerator and denominator of each of the fractions by the number that will give the common denominator. For example, to find out which fraction is larger, 1/2 or 3/7, multiply the denominators to find the common denominator: 2 X 7 = 14. Fourteen will be the common denominator. To change 1/2 to an equivalent fraction with 14 in the denominator, multiply both the numerator and the denominator by seven. To change 3/7 to an equivalent fraction with a denominator of 14, multiply the numerator and the denominator by two, because 7 X 2 = 14. 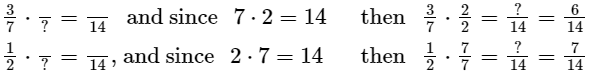
So, 3/7 is equal to 6/14 and 1/2 is equal to 7/14. Because 7/14 is larger than 6/14, 1/2 is larger than 3/7. This method of finding a common denominator may be thought of as multiplying both the numerator and the denominator of each fraction by the denominator of the other fraction.
Calculations using fractions
Addition and subtraction
of fractions can be performed only when the fractions have the same denominator. When the denominators are the same, they name the same sized parts of the whole. You can add sevenths to sevenths to get sevenths. You can subtract thirds from thirds to get thirds. But you cannot add sevenths and thirds, or subtract thirds from sevenths.
To add or subtract fractions that already have the same denominator, add or subtract the numerators, but do not change the denominator. The denominator in the answer will be the same as the denominator of the fractions in the problem. When fractions are added or subtracted, the total number of fractional parts changes, but the size of each of those parts does not change. 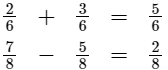
To add or subtract fractions that have different denominators, first rename each fraction to an equivalent fraction so that the new fractions have a common denominator. Then add or subtract. 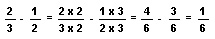
Multiplication
of fractions is similar to multiplication of whole numbers. One meaning for multiplication is that of repeated addition. 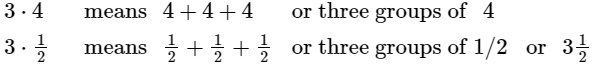
When positive whole numbers are multiplied, the product is larger than either of the original numbers. But when a fraction is multiplied by a fraction, the product is smaller than the original fraction because you are just taking a part of it. 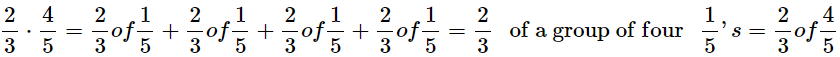
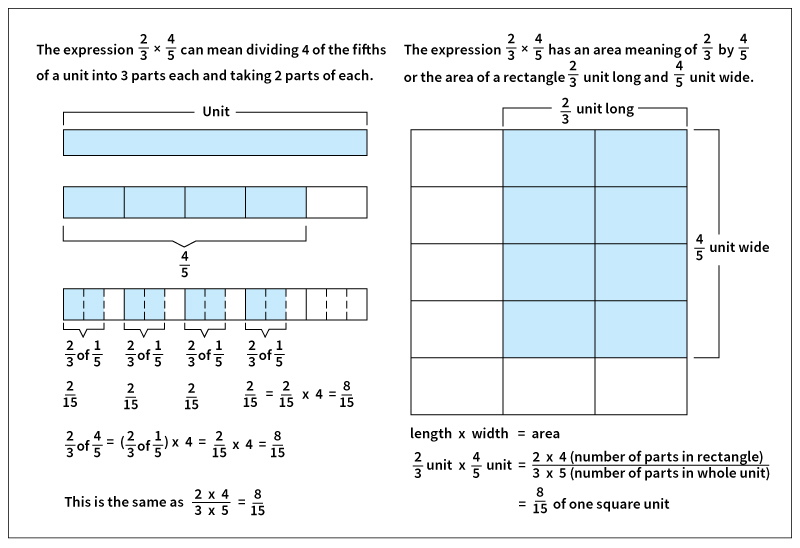
The fraction 4/5 stands for four of the parts formed when a unit is divided into five equal parts. The problem 2/3 X 4/5 means taking 2/3 of each of those four 1/5 ‘s. We can find 2/3 of 1/5 by breaking 1/5 into three equal parts and taking two of them. When a unit has been divided into five equal parts (1/5), and each of these five parts has been further divided into three equal parts (1/3), the result is that the original whole unit has been divided into 15 equal parts, or 1/15 ‘s. Therefore, 1/3 of 1/5 is 1/15. If we take two 1/15 ‘s from each of four 1/5 ‘s, we have 2/3 of 4/5, or 8/15.
To multiply two fractions, multiply their two numerators to get the new numerator. Then multiply their two denominators to get the new denominator. 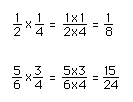
Another meaning of multiplication is that of area—length times width. A card that measures 3 inches wide and 5 inches long, or 3 by 5 (3 X 5) inches, has a total area of 15 square inches. The multiplication of fractions may also be thought of as the expression of area. For example, 2/3 X 4/5 may indicate the area of a rectangle that measures 2/3 unit wide by 4/5 unit long. The area formed by 2/3 unit by 4/5 unit includes eight of the 15 equal parts of the whole square unit. The rectangle therefore has an area that is 8/15 of the area of the whole square unit. This answer is the same as that found by multiplying the numerators and multiplying the denominators of the two fractions.
Often, multiplication of fractions can be made easier by first performing cancellation. Cancellation involves dividing both a numerator and a denominator by the same number. This is the same as dividing a fraction by one, and so it does not alter the answer. When canceling, cross out the old terms and write in the new terms. 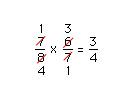
For more information on canceling, see the article on Cancellation.
Division.
A division problem can be rewritten as a multiplication problem. 
The second problem can be rewritten as: 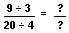
Comparing this problem with the original one, we see that to divide fractions we must divide the numerators to get the new numerator and divide the denominators to get the new denominator. 
However, many division problems do not come out even. 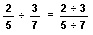
Two cannot be divided evenly by three, and five cannot be divided evenly by seven. Using the division meaning of fractions, we can rewrite the original problem as a complex fraction. A complex fraction has a fraction in its numerator, in its denominator, or in both. 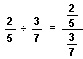
We can simplify this problem by multiplying the fractions in the numerator and the denominator by the inverse of the denominator. The inverse of a fraction is formed by putting its numerator in the denominator and its denominator in the numerator. The inverse of 3/7 is 7/3. The product of any fraction and its inverse is one. 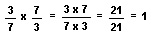
Multiplying both the numerator and the denominator of a complex fraction by the inverse of its denominator is the same as multiplying the complex fraction by one. This operation forms a simpler equivalent fraction with a denominator of 1. 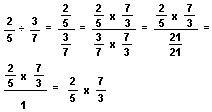
So, 2/5 ÷ 3/7 = 2/5 X 7/3, or 2/5 times the inverse of 3/7. Dividing by a fraction is the same as multiplying by the inverse of that fraction. 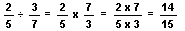
Improper fractions
A fraction that has a numerator that is smaller than its denominator is called a proper fraction. A fraction in which the numerator is equal to or larger than the denominator is called an improper fraction. All improper fractions have a value that is equal to or greater than one. For example, the fraction 27/20 stands for 27 of the parts formed when a unit is divided into 20 equal parts. Since one whole unit contains only 20 of 20 equal parts, 27/20 must be larger than one unit. It is 7/20 more than 1.
The value of the improper fraction 27/20 may also be written as 17/20. Such a number, combining a whole number and a fraction, is called a mixed number. Thinking of the division meaning of fractions helps us understand how to change improper fractions to mixed numbers. For example, 26/3 may be rewritten as 26 divided by 3. 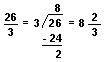
To change a mixed number to an improper fraction, first write the mixed number as an addition problem. For example, the mixed number 52/3 has the same value as 5 + 2/3. The next step is to write the whole number as a fraction. Any whole number can be written in fraction form by using the whole number as the numerator and using 1 as the denominator. Therefore, 5 is written as 5/1. After writing the whole number in fraction form, find a common denominator and add. 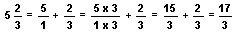
A short cut is to multiply the whole number by the denominator of the fraction. Then add this product to the numerator of the fraction and write the sum as the new numerator. The denominator remains the same. 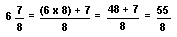
When adding or subtracting mixed numbers, you can write the mixed numbers as addition problems first. Then the whole numbers may be added or subtracted separately from the fractions. 
However, some problems that involve subtraction of mixed numbers are more complicated. 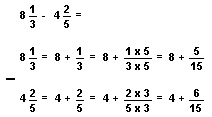
Normally, the next step would be to subtract the whole numbers and then subtract the fractions. But 6/15 cannot be subtracted from 5/15. To subtract these fractions, we must make the top fraction larger. This can be done by borrowing 1 from the 8. If we do so, the whole number becomes 7. Then, we can add the borrowed 1, in the form of 15/15, to 5/15 and subtract the fractions. 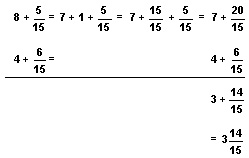
To multiply or divide mixed numbers, change them to improper fractions. Then multiply or divide as usual.
History
More than 4,000 years ago, ancient astronomers in Mesopotamia, now part of Iraq, used fractions made by dividing a unit into 60 parts, then dividing each of these parts into 60 parts, and so on. This system is still used for telling time and for measuring angles in minutes and seconds. The ancient Chinese developed decimal fractions made by dividing units over and over again by 10.
Egyptian mathematicians who helped build the pyramids more than 4,000 years ago used only fractions with 1 in the numerator. Such fractions are called unit fractions. The use of only unit fractions made it necessary to express other fractional parts as sums. For example, 3/4 is expressed in unit fractions as 1/2 + 1/4.
About 2,000 years ago, the ancient Greeks wrote fractions with the numerator on the bottom and the denominator on the top. They did not separate the numerator and denominator by a line. Later, they began writing fractions with the numerator on the top and the denominator on the bottom. Hindu mathematicians in India adopted this method of writing fractions from the ancient Greeks.
During the A.D. 700’s, Arabs conquered parts of India. There, the Arabs learned the decimal system and this method of writing fractions. During the 300 years that followed, the Arabs spread this knowledge through western Asia, across northern Africa, and into Spain.
During the late 1400’s, several arithmetic books that explained the use of fractions and the decimal system were published in Europe. Following the publication of these books, large numbers of Europeans began to use fractions to perform everyday calculations.
Today, fractions are used mostly in connection with inches, cups, pounds, and other measurements in the inch-pound system of measurement customarily used in the United States. However, almost all countries other than the United States use the metric system of weights and measures. The metric system of measurement uses decimal fractions that are written with a decimal point rather than with a numerator and a denominator (see Metric system).
Also, many problems that were once done with fractions using paper and pencil are now done on electronic calculators. These calculators express fractions in the decimal form. As a result of these changes, there are fewer and fewer uses for the fraction form. However, the fraction form continues to be an important means of expressing rates, ratios, and division. The fraction form also continues to be important in algebra and in other special areas of mathematics as a method of writing rational numbers.
Practice fraction examples
1. Bill is 62 1/2 inches tall. Mary is 56 1/4 inches tall. How much taller is Bill than Mary?
2. Sandy’s house stands on a quarter-acre plot. Her father bought the three-eights acre plot next to it. What is the size of the combined plots of land?
3. Mrs. Barry uses 3/4 teaspoon of instant coffee to make one cup. How many teaspoons of instant coffee should she use to make six cups?
4. John wants to saw a board into four equal pieces. He finds that the board is 7 feet 3 5/8 inches long. How long should he make each piece?
5. Lisa can “step off” distances. The average length of her step is 2 1/2 feet. The length of her room measures 7 steps, and the width of her room measures 6 steps. How long is Lisa’s room?
Answers to the practice examples
1. 6 1/4 inches.
2. 5/8 acre.
3. 4 1/2 teaspoons.
4. 1 foot 9 29/32 inches.
5. 17 1/2 feet; 15 feet.
