Arithmetic is the process of calculating by means of symbols called numerals. It is the part of mathematics that concerns how to get answers to addition, subtraction, multiplication, and division problems. The word arithmetic comes from the Greek word arithmos, which means number.

Mathematicians use the term number to mean an idea having to do with the amount or quantity of a thing or things. They use numeral to mean a symbol that represents a number. For example, the numerals 6 and VI stand for the number also represented by the word six. But in everyday language, number is also used to mean numeral. The rest of this article uses number in the everyday way.
Many people use computers and calculators to do most of their arithmetic, but much arithmetic is still done with pencil and paper. Both methods of calculating rely on a numeration system (a system of counting and naming numbers) that determines the value of a digit by its position in a number.

The numeration system used by most people is called the decimal system, or base 10 system. In this system, a digit is any one of the symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Each position in a number with two or more digits has a value 10 times greater than the position to its right. And each position has a name that corresponds to its value. The positions, from right to left, are called the ones’ position, the tens’ position, the hundreds’ position, the thousands’ position, and so on. Each position has only one digit.
A computer or calculator does the actual arithmetic with another numeration system, the binary system. However, the user enters the problem in the decimal system, and the results are shown in the decimal system. This article describes pencil-and-paper procedures for calculating with the decimal system.
Addition
Several methods of addition are in use today. Methods A through C shown here work from right to left. In the United States and Japan, many people use method A. Whenever a column of numerals adds up to 10 or more, you write the digit in the tens’ place above the column to the left. In the example shown, in the ones’ column, 7 + 6 = 13. You take one 10 from the 13 and write it as 1 above the tens’ column. In the hundreds’ column, when you add 8 hundreds and 6 hundreds, you get 14 hundreds. Because 10 hundreds equals 1 thousand, take 10 from the 14 hundreds and add 1 above the thousands’ column.

Method B is similar to method A except that you add the 1 to the top number instead of just writing the 1 above the column. Then you have to add only two numbers, which for most people is much easier than adding three. In the tens’ column, the 4 becomes a 5 when you add the one 10 from the ones’ column.

In method C, all the answer is kept together on or below the line instead of part of it moving above the columns. If the sum of a column is 10 or more, write 1 on the line and then add it to the sum of the next column. In this example, you move one 10 from the 13 in the ones’ column into the tens’ column on the line. In the tens’ column, after adding 4 and 3 for a sum of 7, you add the 1 to the 7 for a total of 8. Method C is easier than method A because you add the two numbers you see above the line and then just increase the sum by 1.
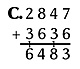
Method D does not require working from right to left. First, add each column. Write the sum at the bottom of each column. In the next step, modify any two-digit answer by adding the number in the tens’ position into the position to the left. For example, take 1 thousand—that is, 10 hundreds—from the 14 hundreds and add it to the thousands’ column. The total in the thousands’ column then becomes 6.

In method E, you add from left to right without writing the numbers carried to the next column. Many Europeans learn method E. Before they write a sum in a column, they look at the next column to the right to see whether it adds up to 10 or more. If it does, they increase the sum of the column on which they are working by 1.
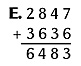
Methods F through H are commonly used by people who have not learned formal calculation techniques. Many people use these methods without writing down any of the steps. In method F, you first add the values in each position—the ones, tens, and so on. Then add the sums for all the positions to get the final answer.
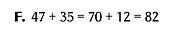
Method G breaks down the process further. You add the numbers in the position of highest value first. In this case, add the 40 from the 47 and the 30 from the 35: 40 + 30 = 70. Then add the 7 from the 47 for a total of 77. Finally, count on the remaining 5 from the 35. People sometimes use equal signs instead of arrows to indicate the accumulating total, but that usage is not correct.
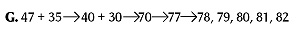
In method H, you adjust numbers to make them easier to add. Increase the 47 by 3 to 50. To balance the increase, decrease the 35 by 3 to 32. Then add 50 to 32.

Subtraction
In method A shown here, you change top numbers to make them larger than bottom numbers. Then you can easily subtract all the bottom numbers from the top numbers. In the example shown, the bottom number in the ones’ column, 7, cannot be subtracted from the top number, 3. So you take one 10 from the top number in the tens’ column and add it to the ones’ position in that number. This addition changes the number in the ones’ position from 3 to 13. In the hundreds’ column, you cannot subtract 8 hundreds from 4 hundreds. So you make the 4 hundreds bigger by adding to it one of the thousands, or 10 hundreds, to make 14 hundreds.

Method A can be used in two ways. In the easier way, you adjust top numbers so that every top number is larger than the number below it. Then you do all the subtraction. You can work from left to right or from right to left. In a more difficult technique, you work one column at a time, starting at the right. You adjust the top number if necessary, then subtract. Schools in the United States commonly teach this technique.
A comparison of subtraction method A and addition method D shows how addition and subtraction are opposite procedures. When doing addition, you can get too many digits in one position and therefore have to add one 10 of the quantity corresponding to that position to the place to the left. When doing subtraction, if you do not have a large enough number from which to subtract, you have to take one 10 of the quantity corresponding to that position from the place to the left.
Method B is similar to method A, but when you take 10 from the left position, you write it as 10. There are two ways to use method B. In the example shown, if you split the 7 in the ones’ column into 3 and 4, you can easily subtract 3 from the 3 to get 0. Then you can subtract the 4 from the 10, which leaves 6. Another approach is to take the entire bottom number from the 10: 10 − 7 = 3. Then you add the difference from that subtraction to the top number: 3 + 3 = 6. Method B comes from Korea.
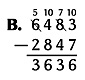
Method C uses equal additions. You add the same amount to the top and bottom numbers so the difference between them stays the same. Schools in Latin America and many European countries teach method C. However, students in some countries do not write the 1’s in the top number.

In this method, you add 10 ones to the ones’ position in the top number to make 13. Then you subtract 7 from 13 to get 6. To balance the 10 ones that you added, you add one 10 to the bottom number in the tens’ column. Write a 1 representing the 10 beside the 4 in the tens’ position. In the tens’ column, first subtract 4 from 8: 8 − 4 = 4. Then subtract the 1: 4 − 1 = 3. In the hundreds’ column, add 10 hundreds to the 4 hundreds in the top number to get 14 hundreds. Then add 1 thousand to the 2 thousands in the thousands’ column.
Methods D and E involve working with numbers that have the same value positions. In method D, you subtract the 200 of the 278 from the 600 of the 634 to get 400. Then, you subtract the remaining 78 from 400 to get 322. Finally, you add to the 322 the 34 left over from the 634 for an answer of 356.
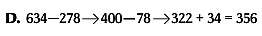
Method E is similar to addition method H. You adjust the numbers to make them easier to use. Adding the same amount to both numbers does not change the difference between them. By adding 2 to both numbers, you get 636 and 280. The number 280 is easier to work with than 278. To count up from 280 to 636, you first count 20 to get to 300, then 300 to get to 600, and then 36 to get to 636. Then add the numbers 20, 300, and 36 for the total difference.
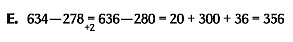
Multiplication
You can multiply by adding repeated copies of a number. Method A requires only that you multiply by 10, 100, or 1,000, and so on, and then add the resulting multiples. Multiplying by 10 moves a number one value position to the left. So 10 times 486 is 4,860. Multiplying by 100 moves each number two value places to the left. So 100 times 486 is 48,600. So 324 x 486 is just four copies of 486, two copies of 4,860, and three copies of 48,600. Add all of these copies together to find the final answer, called the product.

In method B, you multiply each digit in the top number, called the multiplicand, by each digit in the bottom number, called the multiplier. In this example, 486 is the multiplicand and 324 is the multiplier.

Method C is a shortcut of method B in which you multiply the entire multiplicand by each number in the multiplier. You begin on the right. In the example shown, first multiply 486 by 4. Then multiply 486 by the number in the tens’ position in the multiplier: 20 x 486. And then multiply 486 by the number in the hundreds’ position in the multiplier: 300 x 486. Schools in the United States teach method C.
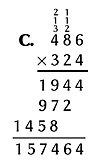
Egyptians used method D more than 2,000 years ago. To use this doubling method, sketch a table with two columns. In the right column, write the multiplicand on top, double it, and write the doubled figure below it. Double this second number and write it as the third number in the column. In the left column, write 1 on top, double it to 2, and write the 2 below the 1. Then double the 2 to 4 and write the 4 below the 2. Continue in this manner until the next number you would write in the left column is bigger than the multiplier.
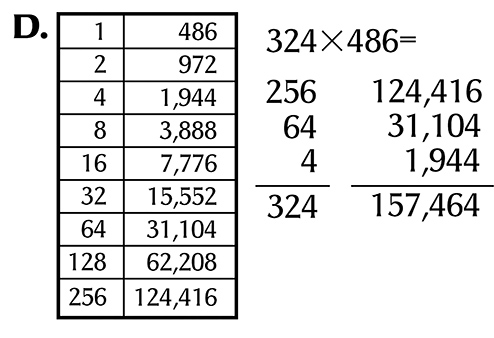
Then, choose the numbers in the left column that add up to the multiplier. Finally, add the corresponding values from the right column. For example, to multiply 486 by 324, add the values for 256, 64, and 4 because 256 + 64 + 4 = 324. The result is the following: 124,416 + 31,104 + 1,944 = 157,464.
Method E has been used in Arab nations, China, India, Japan, and Western Europe. First, draw a rectangle and divide it into rows and columns. Divide each resulting square by a diagonal line running from top right to bottom left. Write the multiplicand, 486, across the top, and the multiplier, 324, down the right side. Write the product of each row and column in the square for that row and column. Place the tens part of the product in the top triangle and the ones part in the bottom triangle.

Then add from right to left. Begin by writing below the square the number in the lower right triangle—in this case, a 4. Then, add the numbers in the diagonally arranged group of triangles that are above and to the left—in the example, the three 2’s. You continue in this manner. If a sum has two digits, write the tens’ digit above the top triangle of the next group. Include that digit when you calculate the sum for that next group.
In the example, the shaded 2 + 2 + 2 = 6 consists of the first group of triangles and its sum. The shaded 2 + 1 + 4 + 1 + 8 + 1 = 7 consists of the tens’ digit from the second group (the 2), the numbers in the entire third group (the 1, 4, 1, 8, and 1), and the ones’ digit of the sum of those six numbers (the 7). The answer to the problem runs from the square’s top left side to its bottom right.
Division
Method A shows the basic method of division. In this method, you take away copies of the divisor (the number by which you are dividing) in multiples of 1, 10, 100, and so on. You continue taking away copies until you use up the dividend (the number you are dividing) and therefore cannot take away any more copies. The answer is called the quotient. There is also usually an amount left over called the remainder. Method A for division is the opposite of method A for multiplication.

Method B resembles division method A, but you take away more than one set of each multiple at a time. You do not need to take away all the sets of a given size in the first try. In the example shown, 3 sets of 100 copies of the divisor could have been taken away in the first try. But actually, 2 sets of 100 copies, then 1 set of 100 copies, were taken away.

In method C, you must take away all the sets of a given size in the first try. In the example, you must begin by taking away 3 sets of 100 copies of the divisor. Schools in the United States usually teach method C.

Method D is an abbreviation of method C. It comes from Argentina and other Latin American countries. Write the divisor on the right, the dividend on the left, and the quotient below the divisor. When you subtract from the dividend, write down only the answer to that subtraction.

Method E became widespread in Europe in the 1400’s. It originated in India, where the calculations were written in sand. Method E resembles method C, except that you write the results of subtraction above the dividend instead of below. This method is shown in three steps so you can see how it works. The work for each step is shaded. Each number is scratched out as it is used.
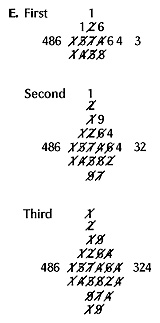
In the first step, multiply 486 by 3. Write the first part of the quotient—3—to the right and the answer—1,458—below the dividend. Then subtract 1,458 from 1,574. Work from left to right (5 − 4 = 1 and 7 − 5 = 2), writing the remainder above the dividend. To make a subtraction in the hundreds’ column, you need to change the thousands’ column. Take 1 from the 2, crossing out the 2 and writing the resulting 1 above it. The 1 that you took away from the thousands’ column becomes a 10 in the hundreds’ column. Mentally add the 10 to the 4 in the hundreds’ column, then subtract 8 from 14.
Arithmetic of small fractions
The addition and subtraction of fractions that are smaller than 1 is similar to the addition and subtraction of whole numbers (numbers that are not fractions). There is a major difference, however, between the multiplication and division of fractions less than 1 and the multiplication and division of whole numbers.
In multiplication, when the multiplier is a whole number larger than 1, the product is larger than the multiplicand. For example, 2 x 3 = 6. However, when the multiplier is a fraction less than 1, the product is smaller than the multiplicand. This result occurs because multiplying a number by a fraction less than 1 means taking a part of that number. For example, 1/2 x 3 means taking one-half of 3, which is smaller than 3.
In division, when the divisor is a whole number larger than 1, the quotient is smaller than the dividend. For example, 6 ÷ 3 = 2. However, when the divisor is a fraction less than 1, the quotient is larger than the dividend. This result occurs because dividing a number by a fraction less than 1 means finding out how many of that fraction are in the number. For example, 3 ÷ 1/2 means, “How many one-halves are in 3?” There are 6, and 6 is a bigger number than 3.
Arithmetic of negative numbers
Negative numbers help describe things that have opposite values, such as wins and losses or income and expenses. Negative numbers also help describe measurements whose amounts are opposite in direction—temperatures above and below zero degrees or heights above and below sea level. One value or direction is considered to be positive and the opposite value or direction negative. Positive numbers have a plus sign; negative numbers, a minus sign.
Because negative numbers are the opposite of positive numbers, the arithmetic of negative numbers differs from that of positive numbers. Adding two positive numbers makes a bigger positive number, and adding two negative numbers makes a bigger negative number. But when a positive number and a negative number are added, the smaller number cancels that much of the bigger number. Whether the sum is positive or negative depends on the sign of the bigger number. If the bigger number is positive, the sum is positive. If the bigger number is negative, the sum is negative. Adding a negative number is equivalent to subtracting a positive number of the same size.
Subtracting a negative or a positive number from a number of opposite sign is the same as adding the opposite kind of number. For example, 10 − (−5) = 15 just as 10 + 5 = 15. And −10 −(+5) = −15 just as -10 + (−5) = −15. Therefore, subtraction does not always result in a smaller number. If you subtract a negative number from a positive number, you will get a larger number because taking away the negative value provides that much more of the positive value.
Multiplying by a positive number can be thought of as repeated addition. Repeatedly adding a negative number results in a larger negative number: 8 x (−3) = −24. Multiplying by a negative number can be thought of as repeated subtraction. Repeatedly subtracting a positive number also gives a larger negative number −3 x (+8) = −24. However, repeatedly subtracting a negative number gives a positive number. Thus, when the signs of the numbers are opposite, a negative number results. When the signs are the same, a positive number results.
Division is the opposite of multiplication. Therefore, to determine the sign of a quotient, you can convert the division problem to a multiplication problem. For example, you can convert −24 ÷ 8 = ? to 8 x ? = −24. You know that multiplying a positive number by a negative number results in a negative number. Therefore, the number represented by the question mark in the multiplication problem—and the division problem—must be negative.
The general rules for division are: Dividing opposite kinds of numbers, one positive and one negative, results in a negative quotient. Dividing like kinds of numbers, both positive or both negative, yields a positive quotient.
History
Calculation tools.
During most of human history, few people used written numbers to calculate. Many numeration systems were difficult to use, especially for multiplication and division. Writing materials were also expensive until the mid-1800’s, when machine-made wood pulp paper became available.
Most ancient people used calculating objects, such as pebbles and sticks, rather than written numbers. An individual manipulated the objects on a board, a cloth, or some other surface. Lines drawn on the surface helped the individual distinguish columns or rows that had different numerical values.
People living in western Africa used a type of small seashell called a cowrie shell for their calculations. The Inca of South America calculated with kernels of wheat on a board. The ancient Greeks and Romans used stones on wood or marble tables. The Chinese and Japanese used small bamboo or wooden reckoning sticks on a board divided into columns. Later, the use of an abacus, a counting device with beads fastened on rods, became widespread in Asia and Russia.
Mechanical calculators that used gears began to appear in Europe in the 1600’s. In the 1940’s, scientists and engineers built electronic calculators using vacuum tubes. As smaller electronic components were developed, electronic calculators became smaller, faster, and cheaper. By the early 1990’s, inexpensive handheld calculators were available throughout the world.
Written arithmetic methods.
The decimal system of numeration made written calculations easy to perform. This system evolved in India sometime between A.D. 600 and 900. Indian and Arabic scientists and mathematicians devised a variety of arithmetic methods based on the decimal system. By 1000, the Arabs had spread these methods throughout their empire, and the methods had begun to filter into Europe.
The development of the printing press in Europe in the mid-1400’s enabled printers to produce inexpensive books. As a result, arithmetic books written in the languages of the common people soon became available. Prior to that time, arithmetic was taught mostly in universities, which used the Latin language. By the 1800’s, young children were learning arithmetic in school in their own language.
Today, the availability of calculators makes it seem unnecessary for older students to memorize and practice complicated arithmetic procedures. But it is important to know how to determine whether an answer obtained on a calculator is reasonable.
