Lens is a piece of transparent material that creates an image of an object by bending light. The image may be larger than, smaller than, or the same size as the object. The human eye has a lens that creates images on the retina, the innermost layer of the wall of the eyeball. Most manufactured lenses are made of glass or plastic. People use them in a variety of applications, including eyeglasses, cameras, microscopes, and telescopes.
Lens shapes
Scientists classify an individual lens as positive or negative, depending on the shape of its cross-section.
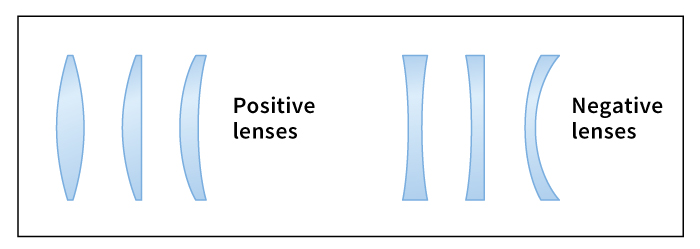
A positive lens
is thicker at the center than the edge. The simplest positive lens manufactured is disk-shaped, and it bulges outward equally on both sides. The lens of the human eye has the same general shape, but the side that “faces the world” is slightly flatter than the back side. Any lens that bulges outward on both sides, equally or not, is a double-convex lens. Convex means curving out.
Other positive lenses have one flat side and one side that bulges outward. Such lenses are commonly used in cameras, microscopes, and telescopes. They are less expensive to produce than double-convex lenses.
Some lenses in eyeglasses are also positive. Both sides of an eyeglass lens curve away from the eye, but one side curves more than the other. Lenses that are used to correct farsightedness are thicker at the center than at the edge, and are therefore positive. Contact lenses that correct farsightedness have the same shape.
A negative lens
is thicker at the edges than in the center. The simplest kind of negative lens is disk-shaped, and it curves inward equally on both sides. Any lens that curves inward on both sides is a double-concave lens. Concave means curving in. Other negative lenses have one flat side and one side that curves inward. Eyeglass lenses and contact lenses that are used to correct myopia (nearsightedness) are thicker at the edges than at the center and are therefore negative lenses.
Creating an image
A lens creates an image by bending light in a process known as refraction. Light travels in waves, which consist of alternating crests and troughs. The crest of an individual wave travels as a wave front that is perpendicular to the wave’s direction of motion. This movement is similar to that of an ocean wave approaching a beach. You can also think of light as traveling in rays along the wave’s direction of travel. At the beach, a surfer riding a wave directly toward shore would represent a ray.
To understand how refraction occurs, imagine that you are holding a glass lens vertically, with its edge resting on a desktop. One side of the lens is facing left, and the other side is facing right. To the left of the lens is a burning candle mounted in a transparent holder. The bottom of the candle lies across the lens’s optical axis, a horizontal line passing through the center of the lens.
Consider a wave front originating at the point on the candle that is on the optical axis and facing the lens. The wave front will diverge (expand) from this point in all directions, except where it is blocked by the candle. Thus, the wave front will resemble an expanding spherical shell. Part of the wave front that travels to the right will strike the lens and enter it. As the wave front enters the lens, the lens will refract it, because light travels more slowly through glass than through air.
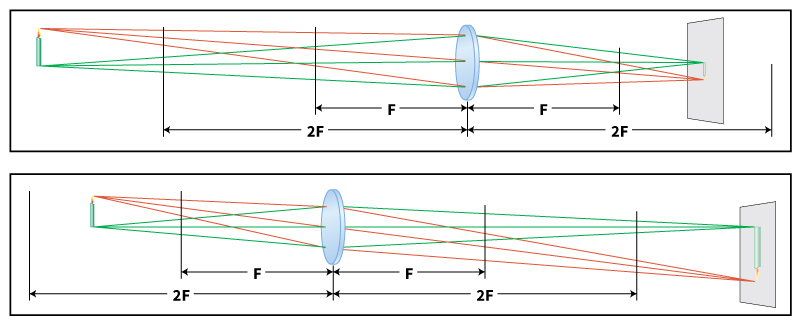
A real image.
Suppose the lens is positive—thicker at the center than the edge. The part of the wave front that travels across the lens’s center will travel farther through glass than will the part traveling across the edge. The center part of the wave front will therefore travel at the reduced speed for a longer time than will the part at the edge. As a result, the light coming through thinner portions of the lens will catch up with, and eventually overtake, the light moving through the center. Due to this activity, the light rays will bend at the surfaces of the lens.
Convergence.
If the candle is far enough from the lens, the wave front will converge (become narrower and narrower) on the right side of the lens. Eventually, it will come together at a point called the focus on the optical axis. The light will then pass through the focus, fanning out as it continues to travel to the right.
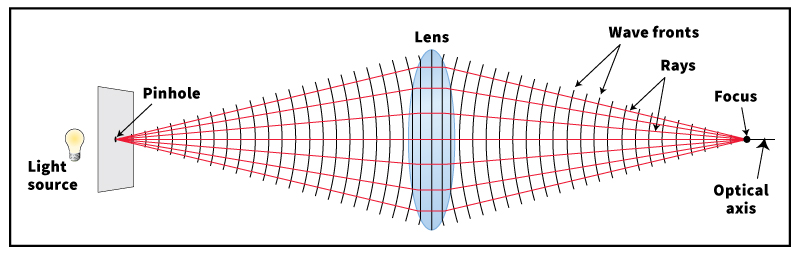
A wave front originating at the tip of the flame will also pass through the lens and converge to a point. But because the flame tip is above the optical axis, this point of convergence will be below the optical axis. Similarly, a wave front from every other point on the side of the candle facing the lens will travel through the lens. Each of these wave fronts will also converge to a point on the opposite side of the axis from its point of origin.
The focal plane.
All the points of convergence will occur in, or close to, an imaginary flat surface known as the focal plane. This surface will be perpendicular to the optical axis. If a motion-picture screen is placed in the focal plane, an image of the candle will become visible on the screen. The image will be inverted—that is, it will be upside down and backward. An image created in this way is known as a real image.
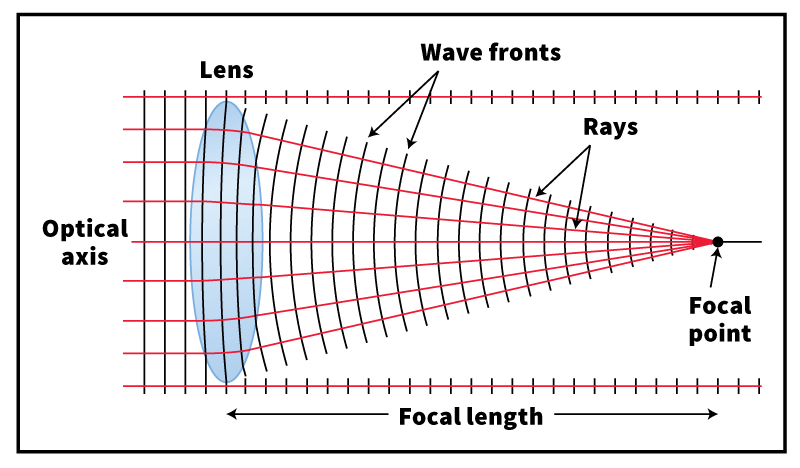
The focal length.
The location of the focal plane and the size of the image will depend on the distance from the object to the lens and on the power of the lens. The power of a lens is defined in terms of its focal length; the more powerful the lens, the shorter its focal length. A lens’s focal length is approximately equal to the distance from the center of the lens to a point known as the focal point of the lens. This is the point of convergence of an incoming wave front that is perpendicular to the optical axis and is neither diverging nor converging when it enters the lens. That is, the incoming light rays are parallel.
The lens equation.
The distance from a positive lens to an object to its left (Do ), the distance from the lens to the corresponding image to its right (Di ), and the lens’s focal length (F) are related according to the following equation, which is known as the lens equation:

If you know two of the factors, you can use the equation to find the third. Suppose the candle is 150 millimeters from the lens, and the focal length of the lens is 50 millimeters. How far is the image from the lens?
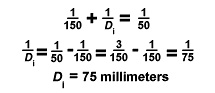
To determine the size of the image relative to the length of the object, divide Do by Di . In our example, the image is two-thirds as long as the candle.
A virtual image.
If the distance from the candle to the lens is equal to the focal length, the lens equation will give you an answer of infinity for Di . This result indicates that a wave front emerging from the lens will not change in width as it travels to the right. Because there will be no convergence, no image can form on a screen, no matter how far the screen is moved to the right.
If the distance from the candle to the lens is less than the focal length, the equation will give a negative answer for Di . A wave front emerging from the lens will continue to diverge. No image can form on a screen.

Viewed through a positive lens.
You can, however, use wave fronts that diverge from a positive lens to create an image. One way to do this is to look through the lens in the direction of the object. The lens of your eye will cause the fronts to converge. You will see an image that is larger than the object and is not inverted. An image created in this way is known as a virtual image. A positive lens used in this way is a magnifying glass.
Viewed through a negative lens.
Suppose the lens in our example is negative. The center part of the wave front will spend less time in glass, and so it will come out of the lens ahead of the remainder of the wave front. The diverging rays entering the lens will therefore diverge more as they leave. As with a magnifying glass, you can create a virtual image by looking through a negative lens. The image will not be inverted, and it will be smaller than the object.
