Binomial theorem is an important algebraic formula. A binomial is an expression that consists of two algebraic terms connected by either a plus sign or a minus sign. For example, (a + b) is a binomial. The expression (a + b)n means that (a + b) is to be raised to the nth power (multiplied repeatedly by itself for a total of n factors). This operation results in an expression called the expansion of the binomial. For example, the expansion of (a + b)2 is a2 + 2ab + b2. The binomial theorem states a rule for writing the expansion of (a + b)n when n is any nonnegative whole number. The binomial theorem can be developed by observing patterns in expansions of (a + b)n as shown in the example below:

Each of the above expansions follows a certain pattern. (1) Each one has (n + 1) terms. (2) The first term is an and the last bn. (3) The exponent of a decreases by 1 in each term and the exponent of b increases by 1. (4) The sum of the exponents of a and b in each term is n. (5) The coefficient of the first term is 1, of the second, n/1, of the third, n(n – 1)/1 X 2, and so on. This pattern enables one to write the expansion in a general form called the binomial theorem as follows:

In general, the letter r can be used to represent the power of b in the expansion. The formula for the term containing br can be written as follows:
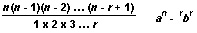
The binomial theorem is used in the analysis of the binomial probability distribution. This distribution describes the possible outcomes of a certain experiment. The coefficients of the terms of the binomial theorem are the same as the elements of the Pascal Triangle. Sir Isaac Newton discovered that if the exponent n is any number other than a whole number, the binomial theorem leads to an infinite series (see Series ).
