Cylinder, in geometry, is a solid figure with two identical bases that lie on parallel planes. Each base is bounded by a curved edge, called the directrix. The lateral surface (side) of a cylinder consists of parallel lines that join corresponding points on each base. When the directrixes of a cylinder are circles, the figure is called a circular cylinder. A right circular cylinder is a circular cylinder with a lateral surface that is perpendicular to the bases. Circular cylinders with a lateral surface not perpendicular to the bases are called oblique circular cylinders. A cylinder whose directrixes are ellipses is called a cylindroid.
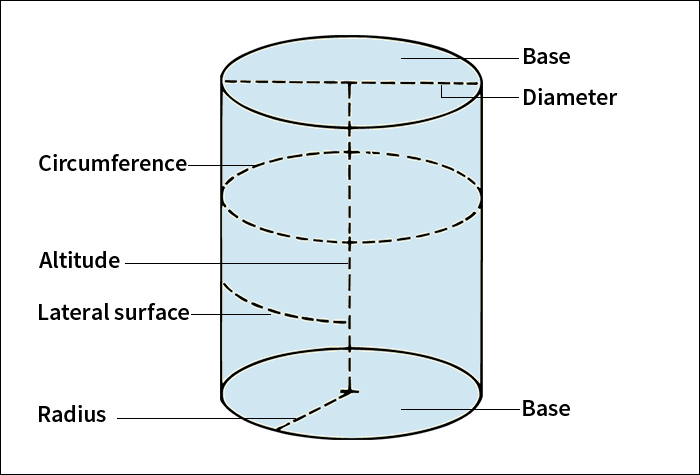
The height (h) of a cylinder is the perpendicular distance between the planes of the bases. The volume (V) of a cylinder can be calculated by multiplying the height by the area (B) enclosed by either of the two bases: V = Bh. If the bases are circles, then B = pi X r-squared, where r stands for the radius of either of the circles. The formula for the volume can then be written: V = pi X r-squared X h. An approximate value for pi is 3.1416.
The area of the lateral surface in a right circular cylinder is equal to the circumference of the base times the height. It can be found using the formula L = 2 X pi X r X h. In the formula, L stands for the lateral surface area. The total surface area (A) of a right circular cylinder, therefore, can be calculated by adding together the lateral surface area and the areas of the two bases: A = (2 X pi X r X h) + (2 X pi X r-squared) or (2 X pi X r) X (h + r).
