Determinant, in mathematics, is a single number related to a square array (arrangement) of numbers called elements. For example, the following array is related to the number 16:
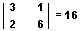
You can compute the value of this determinant in three steps. (1) Multiply the upper left element 3 by the lower right element 6: 3 X 6 = 18. (2) Multiply the lower left element 2 by the upper right element 1: 2 X 1 = 2. (3) Subtract the product of step 2 from the product of step 1: 18 – 2 = 16. The word determinant is also used for the square array itself.
Mathematicians use determinants primarily to solve simultaneous linear equations. These are sets of two or more linear equations in which the variables (unknown numbers) can be satisfied by the same values. Mathematicians also use determinants for solving other kinds of problems, including the calculation of certain areas and volumes.
Using 2 by 2 determinants.
The determinant above is a 2 by 2 determinant because the array has two rows (3,1 and 2,6) and two columns (3,2 and 1,6). In general, the symbols a1, b1, a2, b2 can be used to represent the numbers of any 2 by 2 determinant. Using this notation, the value of the determinant is stated as follows:
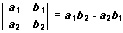
You can use a 2 by 2 determinant to solve simultaneous linear equations involving two variables. Such equations can be written
a1x + b1y = c1
a2x + b2y = c2
The letters x and y represent the variables. You can solve these equations for x and y by arranging the numbers and variables as the ratio of two determinants according to the following formulas.
The formula to solve for x is:
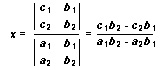
The formula to solve for y is:

The same array appears as the denominator in the formulas for both x and y. This array is called the determinant of the system. It is made up of the coefficients (multipliers) of x and y in the original equation (a1, a2, b1, b2). The numerator in the formula for x is the determinant of the system with the coefficients of x replaced by the constants (numbers without variables) in the original equations (c1, c2). Similarly, these constants replace the coefficients of y in the numerator of the formula for y.
The following equations are simultaneous linear equations involving two variables. These equations can be solved using 2 by 2 determinants.
3x + 1y = 5
2x + 6y = 14
To find the value of x, write the equations as the ratio of two determinants following the formula to solve for x. Then compute the value of the determinants as directed in the first paragraph of this article. The result is
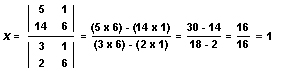
You can solve the equations for y in a similar way.
Using higher order determinants.
The order of a determinant is the number of rows or columns it has. A 2 by 2 determinant is of the second order, a 3 by 3 of the third, and so on. Determinants of an order higher than the second appear, for example, in the solution of three or more simultaneous equations.
You can use third order determinants to solve the following three equations simultaneously:
a1x + b1y + c1z = d1
a2x + b2y + c2z = d2
a3x + b3y + c3z = d3
The formulas for x, y, and z are similar to the ones used to solve only two equations. The denominator of each formula is the determinant of the system. The numerators are the determinant of the system with the coefficients of x, y, or z replaced by the constants (d1, d2, d3). For example, the formula for x is:
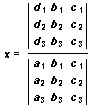
Third order determinants such as the one above can be computed in several ways. One method is to reduce the determinant to a series of 2 by 2 determinants. With this method, the denominator in the above formula can be reduced as follows:
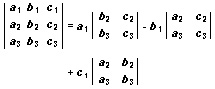
In this operation, each 2 by 2 determinant is multiplied by a number that appears in the first row of the 3 by 3 determinant (a1, b1, c1). The 2 by 2 determinants are called minors of these first row elements. A minor consists of the elements that remain in the 3 by 3 determinant after the row and column in which the number appears are crossed out.
This series of 2 by 2 determinants is called an expansion in terms of the minors of the first row. It consists of the products of the first row elements and their respective minors. The value of the 3 by 3 determinant is computed by alternately adding and subtracting these products.
Determinants of orders higher than the third also can be computed by reducing them to 2 by 2 determinants. Mathematicians use a variety of methods to make the reductions.
