Falling bodies, Law of. Several laws, or rules, tell what an object does when it is allowed to fall to the ground without anything stopping it. These are called the laws of falling bodies. From the time of Aristotle to the end of the 1500’s, people believed that if two bodies of different mass were dropped from the same height at the same time, the heavier one would hit the ground first. The great Italian scientist Galileo did not believe this was true. He reasoned that if two bricks of the same mass fall at the same speed, side by side, they ought to fall at the same speed even when cemented together. Therefore, a single brick would fall just as fast as the heavier two bricks cemented together.

Other scientists disagreed with Galileo. According to a story that probably is not true, he proved his theory about 1590 in an experiment at the famous Leaning Tower of Pisa. Galileo is supposed to have gone to the top of the tower with two cannon balls, one large and the other small. He dropped them both at the same instant, and they reached the ground at nearly the same time. There was a small difference, but not nearly so great as the difference between their weights. Galileo concluded that it was the resistance of the air which caused the difference in time of fall between the two balls. Whether or not Galileo actually conducted this experiment, his reasoning about the result was correct.
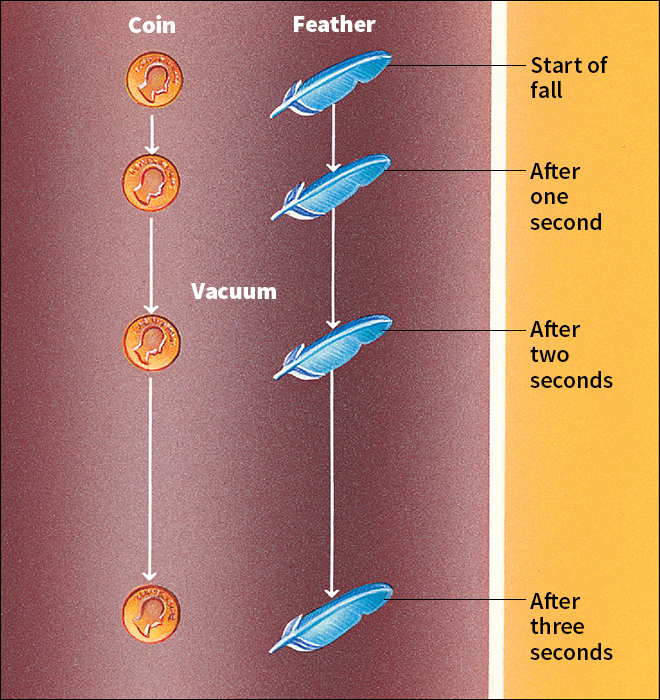
The dispute was not finally settled until the air pump was invented about 1650. Then it was shown that if the air were pumped from a long tube, and a feather and a coin were dropped down the tube at the same instant, they would fall side by side and reach the bottom together. The force which draws bodies toward Earth is called gravity (see Gravitation).
It has been found that the force of gravity acts on all bodies alike, regardless of shape, size, composition, or density. Earth attracts bodies toward its center, so all bodies on Earth tend to fall in a direct line toward that point. This is the direction called down, and it is exactly perpendicular to the surface of still water.
There are three things to consider in studying the laws of falling bodies. One is the distance the body travels when it falls. The second is its velocity, or speed in a given direction. The third is its acceleration, the rate at which its speed increases as it falls (see Motion (Describing motion)). The abbreviations of these three terms are d, v, and a.
The longer a freely falling body falls, the faster it travels. The first law of falling bodies says that, under the influence of gravity alone, all bodies fall with equal acceleration. If the bodies start from rest, and their velocities increase at the same rate, their velocities will remain equal as they fall.
Actually, when various kinds of bodies fall through the air, they fall at different velocities. The air resists the falling bodies, so they are not falling under the influence of gravity alone. You can test this resistance by dropping two sheets of newspaper, one unfolded and the other crushed into a ball. Both pieces have the same weight, so they give a perfect illustration that the difference of shape and not of mass causes the difference in the speed at which various kinds of bodies fall.
The acceleration of a falling body is the same for each second. There are no spurts in its “pickup,” and its fall is described as uniformly accelerated motion. This is true if gravity is the only force acting on the body. Gravity acting on a body that falls from rest increases its velocity during each second of fall by the same amount of velocity that the body had at the end of its first second of fall. The velocity at the end of the first second is 32.16 feet (9.802 meters) per second (at the latitude of New York City). The speed of the body increases at a rate of 32.16 feet per second for each second it falls. The body’s acceleration is expressed as 32.16 feet per second per second. This figure is used in most calculations.
At the end of the 1st second v = (0 [rest] + 32.16) = 32.16 feet per second.
At the end of the 2nd second v = (32.16 + 32.16) = 64.32 feet per second.
At the end of the 3rd second v = (64.32 + 32.16) = 96.48 feet per second.
At the end of the 4th second v = (96.48 + 32.16) = 128.64 feet per second.
A simple formula to get the velocity of a falling body at the end of any second is to multiply the body’s acceleration, a, or 32.16 feet per second per second by the time the body has fallen in seconds, t. This can be written in the form of an equation as:
v = a × t = 32.16 × t
There is also a simple formula to find the distance a body falls in a given second. Multiply the distance it falls the first second by twice the total number of seconds, minus 1. The distance fallen during the first second is always 16.08 feet (4.901 meters), which comes from the value of the acceleration, a, divided by 2. Thus, the distance fallen during the third second is 16.08 feet × [(2 × 3) – 1] = 80.40 feet. The distance fallen during the fourth second equals 16.08 feet × [(2 × 4) – 1] = 112.56 feet. In equation form, the distance traveled in any second is:
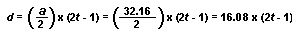
By adding the distance fallen during any given second to the distances for all the preceding seconds, you can find the total distance traveled at the end of that given second. For instance, at the end of the third second, a body has fallen 16.08 + 48.24 + 80.40 feet, which adds up to 144.72 feet. Now 144.72 can also be divided up this way: 3 × 3 × 16.08. The total distance fallen in 4 seconds, 257.28 feet, can be divided this way: 4 × 4 × 16.08. So a shorter formula has been worked out which says that the distance a falling body travels in a given time equals the value of its acceleration divided by 2 and then multiplied by the square of the number of seconds, or 16.08 times the square of the number of seconds.
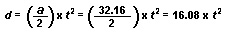
The above three equations are true not only for falling bodies, but for any bodies that have uniformly accelerated motion. Any acceleration, a, can be used instead of 32.16 feet per second per second.
