Fourth dimension. We usually think of space as having three dimensions: length, width, and height. A box that is 6 feet long, 4 feet wide, and 2 feet high can be described by the ordered set of numbers (6,4,2). Such a set may also be used to describe the position of a point in space—for example, the position of an airplane. But three numbers cannot represent the movement of the plane. To indicate when a plane in flight is at a particular location, such as (6,4,2), we need a fourth dimension—time.
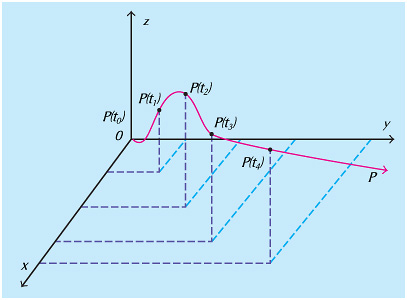
The path of a flying plane can be plotted in four dimensions as shown in the graph, where the plane takes off from point O and travels southeast. The position on the x-axis shows its distance south of point O; the position on the y-axis, its distance east of point O; and the position on the z-axis, its altitude. Curve P represents the path of the plane through space. The points along curve P indicate the location of the plane at four different times, called to to t4
The fourth dimension need not always represent time, however. It may represent anything that we can measure, including temperature and weight.
In the early 1900’s, the German mathematician Hermann Minkowski realized that the special relativity theory proposed by the German-born physicist Albert Einstein described a universe with four dimensions. According to Minkowski, time combines with the three dimensions of space to form space-time. Mathematicians afterward began to study geometries of four or more dimensions. See Relativity .
