Multiplication is a short way of adding or counting equal numbers. Multiplication is one of the four basic operations in arithmetic along with addition, subtraction, and division.
Suppose you want to know how much six gumballs will cost. The gumballs are 5 cents each. You can find the answer by addition: 5 + 5 + 5 + 5 + 5 + 5 = 30. Six gumballs will cost 30 cents. However, it is easier to learn that six 5’s are 30. Learning facts like this is the basis of multiplication.
Learning to multiply
Many people learn multiplication only by memorizing its facts and rules. Often people do not understand the methods that they are using. The best way to learn how to multiply is to find out how multiplication works.
Writing multiplication.
Operations in arithmetic are shown by symbols. The symbol of multiplication is X. The statement 6 X 5 = 30 means “six 5’s are 30.” People also say, “5 multiplied by 6 is 30,” or they can say “6 times 5 is 30.”
The number that is being multiplied, or added together a number of times, is called the multiplicand. The number that does the multiplying, or the number of multiplicands to be added, is called the multiplier. The result, or answer, is called the product. A multiplication problem is usually written like this:

You do not need to write the names, but you must keep the columns straight when multiplying larger numbers. An understanding of place value is important in multiplication. See Decimal system (Multiplication) .
Multiplication facts.
A statement such as 6 X 5 = 30 is a multiplication fact. It consists of a multiplier, a multiplicand, and a product. You should use addition to discover the multiplication facts. For example, 5 + 5 + 5 + 5 + 5 + 5 = 30. After discovering a multiplication fact, you should memorize it. By knowing the 100 multiplication facts, you can learn to multiply any numbers.

Most of the multiplication facts are easy to learn. If you play a game and score 0 four times, your score is 0, because 4 X 0 = 0. Zero multiplied by any number is zero. Any number multiplied by zero is also zero. You have now learned 19 of the multiplication facts!
If you make a score of 1 four times, your score is 4, because 4 X 1 = 4. Similarly, 5 X 1 = 5, 6 X 1 = 6, and 8 X 1 = 8. One multiplied by any number is that number. Any number multiplied by one is also that same number. You now know 17 more multiplication facts.
The two boxes of eggs shown below illustrate an important rule in multiplication. Each box contains 12 eggs. You can look at the box of eggs at the left in two ways. You might say that there are six rows of eggs with two eggs in each row. Or, you could say that there are two rows of eggs with six eggs in each row.

You can also look at the box of eggs at the right in two ways. You might say that there are four rows of eggs with three eggs in each row. Or, you could say that there are three rows of eggs with four eggs in each row. The multiplication facts that show this are:
6 X 2 = 12
2 X 6 = 12
4 X 3 = 12
3 X 4 = 12
The examples of the boxes of eggs illustrate that numbers can be multiplied in any order, which is known as the commutative property of multiplication. The products will always be the same. Knowing this rule cuts down the number of multiplication facts to be learned from 100 to 55.
Knowing the squares is helpful in learning the multiplication facts. A square is a number multiplied by itself. Here are the squares that help to learn the facts:
2 X 2 = 4
3 X 3 = 9
4 X 4 = 16
5 X 5 = 25
6 X 6 = 36
7 X 7 = 49
8 X 8 = 64
9 X 9 = 81
You can make pictures of the squares with dots. Here are the dot pictures of the squares of six and seven:

If you add a row of six dots to the first picture, you will have seven 6’s. This shows that 36 + 6 = 42 or 7 X 6 = 42. If you take away a row of dots from the second picture, you will have six 7’s. This shows that 49 – 7 = 42 or 6 X 7 = 42. Making dot pictures can help you learn the multiplication facts. For example, you can make a square with four dots to show 2 X 2. Another square with nine dots shows 3 X 3. A third could show 4 X 4, and so on.
Learning the multiplication facts takes time and study. But knowing the multiplication facts is necessary to become skilled at multiplying. You can become even better at arithmetic if you learn the division facts as you learn the multiplication facts. The division facts are the opposite of the multiplication facts.
Multiplying by one digit
Any number from 0 to 9 is called a digit. The number 26 is a two-digit number. The number 514 is a three-digit number. A digit gets its value from the place it occupies in a number. The first place on the right is for 1’s, the next to the left is for 10’s, the next for 100’s, and so on. For example, in the number 347, the 3 means three 100’s, the 4 means four 10’s, and the 7 means seven 1’s. Depending on its place, the digit 2 may mean two 1’s, (2), two 10’s (20), two 100’s (200), or two 1,000’s (2,000). You combine the idea of place value with the multiplication facts to multiply large numbers.
Here is an example of the steps needed to work a multiplication problem using more than one multiplication fact. There are 32 students in a class. Each student uses one sheet of paper a day. How many sheets of paper will be needed for three days? We could solve the problem by using addition: 32 + 32 + 32 = 96. The class will need 96 sheets of paper for three days. Multiplication is quicker and easier. The number 32 is three 10’s and two 1’s. The basic idea is to multiply first the 1’s by 3 and then the 10’s.
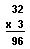
First, you multiply the two 1’s by 3. This is 3 X 2 = 6. You write the 6 in the 1’s place in the product. Next, you multiply the three 10’s by 3. This is 3 X 30 = 90. The 90 is nine 10’s, and you write the 9 in the 10’s place in the product. The answer is 96.
You multiply a larger number by one digit in much the same way:
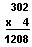
First, you multiply the two 1’s by 4. This is 4 X 2 = 8. You write the 8 in the 1’s place in the product. Next, you multiply the 0 or “no” 10’s by 4. This is 4 X 0 = 0. You write the 0 in the 10’s place in the product. Then you multiply the three 100’s. This is 4 + 300 = 1,200. You write the 12 in the 100’s and 1,000’s place in the product. The answer is 1,208.
When you multiply a large number by one digit, you must multiply each digit of the larger number–the 1’s, 10’s, 100’s, 1,000’s, and so on–one at a time. As you multiply, write down the products of each of these multiplications–the 1’s, 10’s, 100’s, 1,000’s, and so on.
How to carry in multiplication
Students learn how to “carry” when they learn addition. When you add several numbers, there may be a 10 in the sum of the 1’s column. You carry or add this 10 to the 10’s column, usually by writing a small 1 above the 10’s column. Carrying in multiplication is similar to carrying in addition:

When you add the eight 12’s, the eight 2’s total 16, or one 10 and six 1’s. You write the six 1’s in the 1’s place in the sum. You add the 10 to the column of eight 10’s by writing a 1 at the top of that column. Adding the 1’s in the 10’s column gives you nine 10’s. You write nine 10’s in the 10’s place in the sum. To multiply 8 X 12, you multiply the 1’s first. This is 8 X 2 = 16. You write the six 1’s in the 1’s place in the product. You write a 1 to be added to the product of 8 X 1 in the 10’s place. This is 8 X 1 = 8 and 8 + 1 = 9. You write the nine 10’s in the 10’s place in the product. Be sure to multiply first. Then add the “carry number” to the product.
Multiplying by large numbers
A multiplier that has more than one digit introduces a new idea in multiplication. This idea is the use of the partial product. You can learn this idea best from an example.
Jim wants to know how many cartons of milk his school used last month. It used 312 cartons each day for 23 days.

The multiplier, 23, has two digits. It has two 10’s and three 1’s. You must use these as separate parts. First, you multiply 312 by the three 1’s. This is 3 X 2 = 6. You write the 6 in the 1’s place in the product. Then, 3 X 1 = 3 and 3 X 3 = 9. You write the 3 and the 9 in the 10’s and 100’s places in the product. This product of 3 X 312 is a partial product. Next, you multiply 312 by the two 10’s. You write the product of this multiplication below the first product. You start this new partial product one place to the left, in the 10’s place, because 312 is now being multiplied by 10’s, not by 1’s. First, 2 X 2 = 4. This is four 10’s. You write the 4 below the 10’s place in the first product. Next, 2 X 1 = 2 and 2 X 3 = 6. You write the 2 and the 6 in the 100’s and 1,000’s places of the second partial product. Now, the two partial products must be added together. The first partial product is 3 X 312 or 936. The second partial product is 20 X 312 or 6,240. Thus, 936 + 6,240 = 7,176. The answer is that the school uses 7,176 cartons of milk in 23 days.
Multiplying by a three-digit multiplier is the same as by a two-digit multiplier. But there are three partial products instead of two. When you use the 100’s part of the multiplier in a problem with a three-digit multiplier, remember to write this product beginning in the 100’s place.
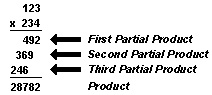
Notice that the partial product of 2 X 123 is started in the 100’s column directly under the 2. You do not write “carry numbers” when you are multiplying by larger numbers. You must carry in your mind. If you wrote in carry numbers, you could easily confuse them with the carry numbers from another part of the multiplier.
Multiplying by zero
Zeros in combination with other digits represent 10’s, 100’s, 1,000’s, and so on. When there are zeros in a multiplier, you can shorten the work of multiplication.
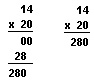
In the example at the right, you can see that there will be no 1’s in the 1’s place. So you can write a 0 to show the 1’s place, and write the product of the two 10’s on the same line. This shortens the work. When you use this method with a three-digit multiplier that ends in zero, the difficulty comes in placing the second partial product:
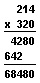
You begin the second partial product in the 100’s place, because 3 represents 100’s. Always check the place of the multiplier when you write its partial product.
An easy way to multiply by 10, 100, 1,000, and other multiples of 10 is to annex zeros. This means to place zeros at the end of a number.
10 X 2 = 20
100 X 2 = 200
1000 X 2 = 2000
Stated as a rule, this means that to multiply by 10, annex a zero to the multiplicand. To multiply by 100, annex two zeros to the multiplicand. To multiply by 1,000, annex three zeros to the multiplicand. You can extend this: 400 X 12 = 4,800
You multiply 12 by 4, and annex two 0’s.
When you multiply larger numbers, there may be a zero in the 10’s place of the multiplier.
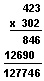
In this case, you write a zero in the 10’s place of the second partial product. This is to make sure you start the next partial product in the 100’s place.
How to check multiplication
You should always check the answer in multiplication to be sure you have solved the problem correctly. You have seen that numbers can be multiplied in any order and the product remains the same. For example, 2 X 4 = 8 and 4 X 2 = 8. The best way to check a product is to change the places of the multiplier and multiplicand and do the multiplication again.

The products are the same, but the partial products are different. If you make a mistake one way, you probably will not make it the other way. If your answers are different, you can locate your mistake. When you multiply a large number by one digit, you can check it easily by dividing the product by the single digit.
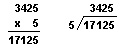
Multiplication rules
These five rules will help you solve problems.
- Remember that multiplication is a short way of adding equal numbers. The multiplier tells you how many times a number is to be multiplied.
- Learn the meaning of the multiplication facts and learn to recall the facts quickly. Remember that a number multiplied by zero is zero and that a number multiplied by one is the same number. Also remember that zero multiplied by any number is zero.
- Remember the methods for multiplying by one or more digits. You multiply the 1’s, 10’s, 100’s, and 1,000’s of the multiplicand one after the other and write the result in the product. When the multiplier has two or more digits, you must use partial products.
- Place value has great importance in multiplication. Always keep the columns straight, and start the product under the digit you are using in the multiplier.
- Learn to check the answer after working a problem in multiplication. You can do this by changing the places of the multiplier and multiplicand, and doing the multiplication again.
Fun with multiplication
Many of the games that can be played using the addition, subtraction, and division facts can be changed a little for the use of multiplication facts.
Product!
is played by a group of children sitting in a circle. The leader picks a number, such as 5. The player next to the leader begins with 1, and the group counts around to the left. When the counting comes to a product of 5, the player calls “Product!” instead of the number. The counting goes like this: “1, 2, 3, 4, Product!, 6, 7, 8, 9, Product!” , and so on. A player who forgets to say “Product!” is out, and the winner is the last player left.
Finger multiplying
can be fun. By using fingers, you can multiply 5, 6, 7, 8, or 9 by 5, 6, 7, 8, or 9.
Suppose you want to multiply 8 X 6. Close the fingers of both hands. Open 3 fingers on the left hand. The 5 closed on the right hand and the 3 open stand for 8. Now open 1 finger on the right hand. The 5 that were closed and the 1 now open on the right hand stand for 6. Now 3 fingers should be open on the left hand and 1 finger open on the right. This is the 10’s digit of the answer. Add the fingers open: 3 + 1 = 4. There are four 10’s in the answer. The closed fingers give the 1’s digit. There are 2 fingers closed on the left hand and 4 fingers closed on the right hand. Multiply these to get the 1’s digit. This is 2 X 4 = 8. Add the 10’s and the 1’s. Four 10’s and eight 1’s are 48. This shows that 8 + 6 = 48.
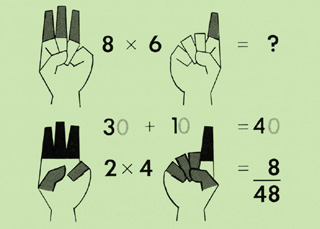
Another example is 9 X 7. Start with the fingers closed. Open 4 fingers on the left hand for 9 (4 + 5 = 9). Open 2 fingers on the right hand for 7 (5 + 2 = 7). Add the fingers open: 4 + 2 = 6. This is the 10’s digit. There is 1 finger closed on the left hand and 3 fingers closed on the right hand. Multiply these for the 1’s digit. This is 1 X 3 = 3. Add the six 10’s and the three 1’s: 60 + 3 = 63. This shows that 9 X 7 = 63.
