Scientific notation is a method used in scientific work to express extremely large or small numbers. Scientific notation provides a compact way to write such numbers and shows how precisely a number is known. This method also makes it easier to perform calculations involving very large or small numbers. Scientific notation states a number as a product of a number from 1 to 10 and a power of 10.
Powers of 10 used for large numbers are products of one or more multiplications in which 10’s are the only factors. The number of times 10 is used as a factor is called the power. For example, the number 1,000,000 equals 10 to the sixth power because: 1,000,000 = 10 * 10 * 10 * 10 * 10 * 10
“Ten to the sixth power” is written 106. The small numeral 6, which indicates the power, is called an exponent. As this example shows, powers of 10 make it possible to write large numbers in a compact way.
To express a large number in scientific notation, move the decimal point to the left from the end of the number to after the first digit. Next, count the number of places that you moved the decimal point. Finally, write a multiplication sign followed by a power of 10. The exponent in the power of 10 will equal the number of places that you moved the decimal point.
For example, the average distance between the earth and the sun is about 150,000,000 kilometers. The decimal point is understood to follow the last zero but is usually not written. To change 150,000,000 into scientific notation, move the decimal point from behind the last zero to after the 1. Next, determine the exponent by counting the number of places that you moved the decimal point–in this case, eight places. Finally, write a multiplication sign followed by 108. Thus, 150,000,000 becomes 1.5 X 108.
Just as large numbers can be expressed in terms of powers of 10, so small numbers can be expressed in terms of powers of 1/10 . Because 1/10 = 10-1, the number of times 1/10 is used as a factor is indicated by a negative power. For example, the number 0.0001 equals 10 to the minus fourth power because: 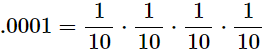
“Ten to the minus fourth power” is written 10-4. Thus, negative powers of 10 make it possible to write small numbers in a compact way.
To express a small number in scientific notation, move the decimal point to the right so that it follows the first number that is not a zero. Then count the number of places you moved the decimal point and write a multiplication sign followed by a negative power of 10.
For example, the diameter of a virus is about 0.000001 centimeter. To write this number in scientific notation, first move the decimal point behind the 1. Then determine the negative exponent by counting the number of places you moved the decimal point–in this case, six places. Finally, write a multiplication sign followed by 10-6. Thus, 0.000001 becomes 1 X 10-6.
The number 10 expressed as a power of 10 is simply 101. Thus, the number 20 can be written as 2 X 101, but scientists usually do not bother to do this. Likewise, the term 100 equals 1, but scientists rarely use this term.
Significant figures.
Scientific notation does more than save space. It also indicates how precisely you know a number. For example, suppose you estimate that you have eaten 14,248 meals in your lifetime. With scientific notation, you can use significant figures, also called significant digits, to indicate the exactness of your answer. Significant figures are the digits to the left of the multiplication sign of a number written in scientific notation. Scientists assume that you are certain of the values of these digits but not the next one.
For example, you could express the number 14,248 as 1.4 X 104. Here you have two significant figures, the 1 and the 4. Your use of 1.4 indicates that you are sure of the value of these two numbers but doubtful about the next one. Thus, 1.4 X 104 indicates that you have eaten about 14,000 meals, but you may have eaten as few as 13,500 or as many as 14,499. If you used four significant figures and wrote your number as 1.424 X 104 you would indicate that you have eaten about 14,240 meals, but you could have eaten as few as 14,235 or as many as 14,244.
You can also use a symbol called a plus-or-minus sign (±) to indicate how precisely you know a number. This method is less compact but more direct than using significant figures. For example, to indicate that a number lies somewhere in the range from 14,235 through 14,245, you could write 14,240±5.
Mathematical calculations.
To add or subtract numbers in scientific notation that have the same exponent, simply add or subtract the significant figures: 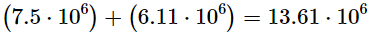
After you complete a problem with numbers in scientific notation, you must put the answer into standard scientific notation. In standard scientific notation, the number to the left of the multiplication sign must be equal to or greater than 1 and less than 10. Also, the result of an addition or a subtraction should have no significant digit farther to the right than the last significant digit in the least precisely known number. The result of a multiplication or a division should have no more significant digits than the number of significant digits in the least precisely known number.
The above answer violates the first two rules. The number to the left of the multiplication sign, 13.61, has a digit–the last “1”–that is farther to the right than the last digit in the least precisely known number in the problem–7.5. To correct this, round off 13.61 to 13.6. Then express the number in scientific notation by dividing the left part by 10 and multiplying the right part by 10. This keeps the value of the number unchanged and puts the number in proper form: 1.36 X 107.
To add or subtract numbers with different exponents, you must first make the exponents the same. If two numbers have different exponents, multiply and divide the two parts of one of them by 10 to make the exponents the same. Then simply add or subtract the significant figures and round off, as in the following example: 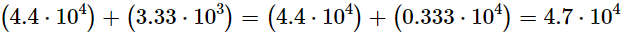
To multiply two numbers in scientific notation, multiply their digits and add their exponents: 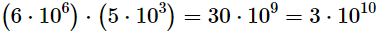
To divide two numbers in scientific notation, divide their digits and subtract their exponents: 
