Series, in mathematics, is the sum of the terms of a sequence. For example, the set of numbers 2, 4, 6, 8, 10 form a sequence. If you add these numbers together, they form the series 2 + 4 + 6 + 8 + 10. A sequence can be any set of terms (numbers or algebraic expressions) arranged in a specific order. An example of a sequence with algebraic terms is a, ar, ar2, ar3, ar4. The related series is a + ar + ar2 + ar3 + ar4. A series such as 1/2 – 1/3 + 1/4 – 1/5 + … contains both positive and negative terms.
Mathematicians name series in a variety of ways to describe how the terms are formed. They call the series 2 + 4 + 6 + 8 + 10 an arithmetic series. Each term of an arithmetic series is formed by adding a certain quantity to the preceding term. In this example, the quantity added is 2. (The sequence 2, 4, 6, 8, 10 is called an arithmetic progression.) The series a + ar + ar2 + ar3 + ar4 is an example of a geometric series. Each term of such a series is formed by multiplying the proceeding term by a certain quantity called the common ratio. In this example, the common ratio is r. (The sequence a, ar, ar2, ar3, ar4 is called a geometric progression.)
Other common types include power series, trigonometric series, and factorial series. The terms of a power series contain some quantity raised to successively higher powers. The simplest power series is 1 + x + x2 + x3 + x4 + x5 and so on. The terms of a trigonometric series contain such expressions as sines and cosines of angles. A simple factorial series has the form 1 + (1 X 2) + (1 X 2 X 3) and so on. When written in factorial notation, this series appears as follows: 1! + 2! + 3!.
Series that become important mathematical tools are often named for the individuals who develop them. Fourier series are used in physics in the study of waves (see Fourier, Joseph Baron ). Taylor series contributed to the growth of calculus.
All series are either finite or infinite, depending on the number of terms they have. A finite series has a definite number of terms that you can count. For example, the series 2 + 4 + 6 + 8 + 10 is a finite series because it has only 5 terms. An infinite series goes on indefinitely so that you cannot count the number of terms. For example, the sum of all the numbers used in counting by 2’s is an infinite series. It is written: 2 + 4 + 6 + 8 + 10 + …
The dots at the end of the series indicate that there is no “last” term. Instead, an infinite number of terms follow the ones that are written.
Working with finite series
The most common questions asked about a finite series are: (1) What is the value of a certain term? (2) What is the sum of a certain number of terms? For example, suppose you want to find the 7th term in the sequence of odd numbers (1, 3, 5, 7, 9, and so on). You can find the answer by merely writing out the following sequence of numbers: 1, 3, 5, 7, 9, 11, 13
The example shows that the 7th term is 13. In a similar way, you can find the sum of the first 7 terms in the related series: 1 + 3 + 5 + 7 + 9 + 11 + 13 = 49
Adding the terms shows that the sum is 49.
You can also use mathematical formulas to find terms and sums of many series. The formulas are especially helpful when you must work with a large number of terms. In the formulas, the letter n usually represents the number of a term. For example, the formula for the _n_th term (Un) in the sequence of odd numbers is Un = 2n – 1
Using this formula, you can calculate the 7th term in the sequence as follows: U7 = (2 * 7) – 1 = 14 – 1 = 13
This is the same answer that you obtain when you write out the sequence of numbers. The mathematical formula for the sum of the first n terms (Sn) of the odd-numbered series is Sn = n2
The sum of the first 7 terms is therefore S7 = 72 = 49
Again, your answer agrees with the sum you obtain by adding the terms.
Mathematicians have developed similar formulas for finding terms and sums of many kinds of series. For more information about finding terms and sums of progressions, see the article on Progression .
Working with infinite series
Probably the simplest infinite series is a geometric series whose common ratio is less than 1. For example, the following geometric series has a common ratio of 1/2: 1 + 1/2 + 1/4 + 1/8 + 1/16 + …
How do you find the sum of this series if it has an infinite number of terms? You can start by making a table showing the sum of the first two terms, the first three, the first four, and so on.

The table shows that the sum gets closer to 2 as you add more terms. If you add enough terms, you can make the sum come as close to 2 as you wish. But the sum never reaches 2. The number 2, then, is called the limit of the sum of n terms as n increases without bound. You can express this statement with mathematical symbols as follows: 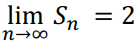
The symbols n→∞ signify that the number of terms increases without bound. Such a limit may also be called merely the “sum” of the series.
You can use mathematical formulas to prove that the sum of this series is 2. The formula for the sum of n terms (Sn) of any geometric progression is:
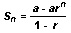
In this formula, a represents the first term of the series, r the common ratio, and n the number of terms. The expression in the preceding column can also be written as two terms:

Consider the second term in the above formula. Let the common ratio, r, be any number less than 1. Then, as the number of terms, n, increases without bound, the factor rn approaches zero. The limit of the second term is therefore zero. (You may want to tabulate some values for the second term to see why this is so. Make r any value less than 1. Then calculate the value of the second term for several increasing values of n. )
The second term of the formula is zero only when n increases without bound. Therefore, we must write:
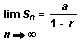
To put this formula to work, we merely insert the proper values. In our example, a = 1, and r = 1/2:
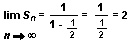
The formula shows that the limit of the sum is 2, the same number arrived at when the series of terms was tabulated.
When the sum of a series approaches a limit as the number of terms increases without bound, the series is said to converge. Otherwise, the series is said to diverge. Mathematicians can prove that many series converge. However, even though convergence can be proved, it is often difficult or impossible for mathematicians to develop a formula for the sum. In such cases, the sum must be obtained approximately by adding terms in the series. In this way, mathematicians calculate many important quantities. These quantities include the trigonometric functions; logarithms; and mathematical constants such as π and e (the base of the natural logarithms).
One of the early expressions for π was developed by the Scotch mathematician James Gregory (1638-1675): π = 4(1 – 1/3 + 1/5 – 1/7 + 1/9 – 1/11 + …)
The terms of this series form a harmonic progression. Gregory’s series converges slowly. This means you have to add a large number of terms to extend the accuracy only slightly. Today, mathematicians use other series that converge more rapidly to the value of π. The expression below shows π carried out to 20 decimal places: π = 3.14159265358979323846
With rapidly converging series and the aid of high speed computers, mathematicians can obtain a value of π correct to tens of trillions of decimal places.
Working with odd numbers
Consider the formula for the sum of the series of odd numbers (1 + 3 + 5 + 7 + … ): Sn = n2
This formula points out a remarkable fact: the sum of n successive odd numbers is always a perfect square. The table below illustrates this fact.
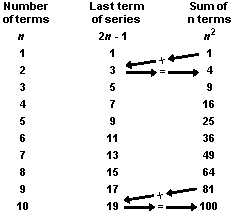
The arrows in the table show the relation between the perfect squares and the successive odd numbers. Followers of the Greek mathematician Pythagoras knew this relationship as early as 540 B.C. They discovered it while studying figurate numbers. Figurate numbers are dots arranged in the form of squares, triangles, and other geometrical figures. For example, the Pythagoreans represented the first 4 perfect squares as follows:
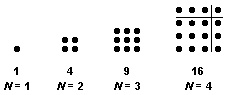
They saw that to form each new perfect square they had to add an odd number of dots to the preceding square. The number of added dots increased by 2 each time. Thus, the dots formed a sequence of odd numbers. To the number 1, the Pythagoreans added 3 dots to make 4, then added 5 more dots to make 9, and so on. The last diagram shows how the Pythagoreans formed 16 by adding dots to 9. They added (1) 3 dots in a row along the top; (2) 3 more in a column on the right side; and (3) a single dot in the upper right corner. The total number of dots added was (2 X 3) + 1 = 7, an odd number.
In general, N can be used to represent the number of dots in a row or column of any square number. Then, to form the next square, one has to add (1) N dots in a row along the top; (2) N more in a column on the right side; and (3) a single dot in the upper right corner. The total number of dots added would be (2N + 1), which is always an odd number. With each new square, N increases by 1. As a result, the number of added dots (2N + 1) increases by 2. Thus the number of added dots forms a sequence of odd numbers. Also, each perfect square is the sum of a certain number of terms in the odd-number series.
